Доказательства и свойства вертикальных углов

Две пересекающиеся в одной точке линии встречаются не только в математике, но и в повседневной жизни. Мы можем наблюдать их, смотря на ножницы, на две скрещенные прямые веточки деревьев. Мы регулярно встречаем их в архитектурных объектах, машиностроении, в различных механизмах и других предметах. Примеров может быть масса. Образованные углы при пересечении составляют основу геометрии и изучаются детьми в средних классах.

Определение вертикальных углов в математике
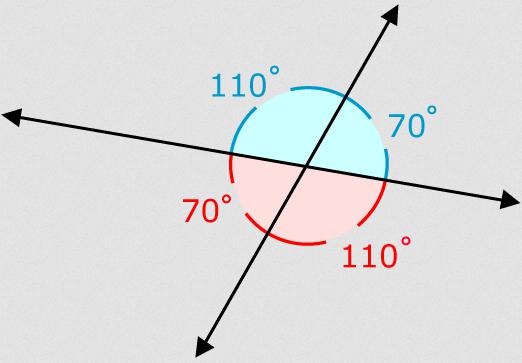
Вертикальные углы - это два угла, образованных путем пересечения двух прямых линий в одной точке. Стороны одного угла в таком случае всегда являются продолжением другого. Таким образом, вертикальные углы находятся напротив друг друга в пересекающихся прямых с общей точкой пересечения.
Свойства вертикальных углов
Решая различные задачи по геометрии, ребенку первоначально необходимо определить, с чем он имеет дело. То есть, перво-наперво он изучает форму фигуры, с которой начинает работу. Для этого он опирается на свойства всех ему известных фигур. Свойства вертикальных углов помогают легко составить в голове алгоритм для решения задачи:
- Две прямые, пересекаясь между собой в одной точке, образуют две пары углов.
- Образованные друг напротив друга вертикальные углы равны.
- Сумма всех углов при пересечении двух прямых в одной точке равно 360°.
- Смежные углы составляют половину вертикальных углов.
При построении прямых линий с одной точкой пересечения образуется два вертикальных угла и четыре смежных. Одно из доказательств равности вертикальных углов - это равность суммы градусов 1 + 2 угла и 3 + 4. Как в смежных, так и в вертикальных углах, если известен один из углов, то второй можно вычислить нехитрым способом. Зная, какими свойствами вертикальные углы наделены, можно быстро определить второй угол. Если из 180° вычесть известный угол, то мы узнаем величину второго.
Похожие статьи
- Особенности российской модернизации начала 20 века. История России
- Характеристика Льва-женщины. Знак Зодиака Лев: описание
- Белоруссия или Беларусь: как правильно говорить и писать?
- Легенда и миф о Зевсе кратко для учащихся 5 класса
- Устное народное творчество: виды, жанры произведений и примеры
- Простое предложение. Виды простых предложений
- Мифы Древней Греции: краткое содержание и суть
