Вычисление площадей фигур в геометрии
Геометрия изучает формы и размеры объектов окружающего нас мира. Одной из важнейших числовых характеристик геометрической фигуры является ее площадь. Знание формул для вычисления площадей позволяет решать множество практических задач в строительстве, архитектуре, дизайне, инженерии. Без понимания принципов вычисления площадей невозможно представить современную науку и технику.
Основные понятия
Площадь фигуры - это числовая характеристика, показывающая размер части поверхности, ограниченной контуром данной фигуры. Площадь измеряется в квадратных единицах, таких как квадратные метры, квадратные сантиметры и т.д.
Площади равных фигур равны. Их периметры тоже равны.
Чтобы найти площадь сложной фигуры, ее можно разбить на несколько простых, площади которых легко вычислить по известным формулам. Затем площадь всей фигуры будет равна сумме площадей ее частей.
Формулы для простейших фигур
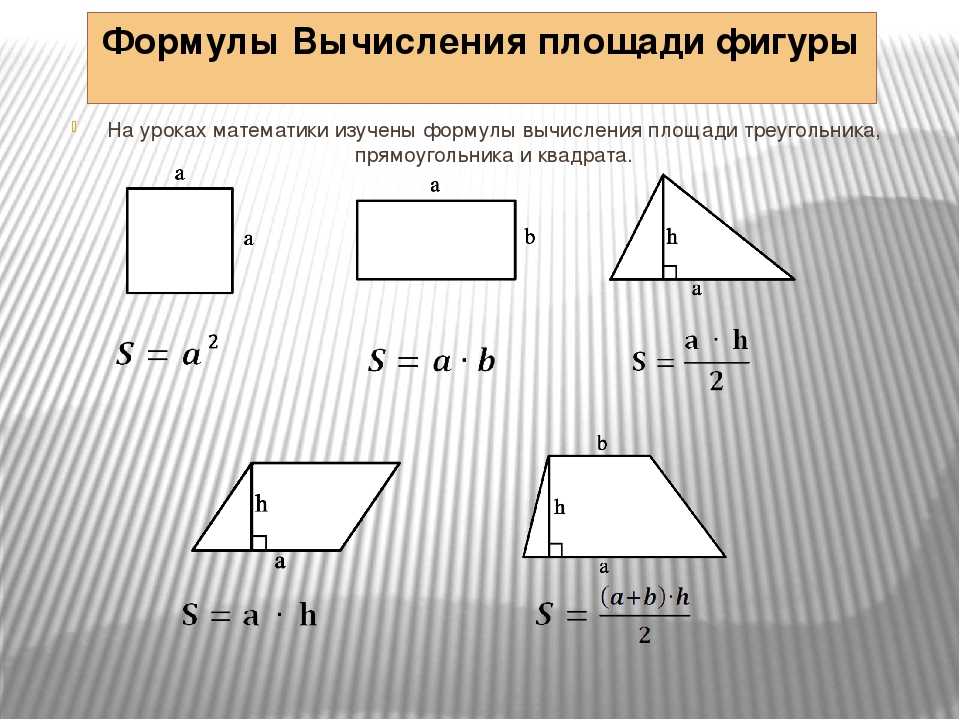
Для вычисления площади квадрата нужно умножить длину его стороны на саму себя:
S = a * a
где S - площадь квадрата, а - длина стороны.
Например, если сторона квадрата равна 5 см, то его площадь равна:
S = 5 * 5 = 25 кв.см
Для вычисления площади прямоугольника используют формулу:
S = a * b
где a - длина прямоугольника, b - ширина.
Например, если длина прямоугольника 10 см, а ширина 5 см, то:
S = 10 * 5 = 50 кв.см
При вычислении площади важно следить, чтобы длина и ширина были выражены в одинаковых единицах измерения.
Формулы для треугольников
Для вычисления площади треугольника используется формула:
S = (a * h) / 2
где a - длина основания, h - высота, проведенная к этому основанию.
Формула Герона позволяет найти площадь треугольника, зная только длины его сторон.
Площадь треугольника можно также вычислить по формуле:
S = (a * b * sin(α)) / 2
где a и b - длины двух сторон, α - угол между ними.
Рассмотрим пример. Дан треугольник со сторонами 5 см, 6 см и 7 см. Требуется найти его площадь.
По теореме Пифагора находим угол α:
α = arccos((5^2 + 6^2 - 7^2) / (2 * 5 * 6)) = 36,87°
Подставляем в формулу:
S = (5 * 6 * sin(36,87°)) / 2 = 10,33 кв.см
Ответ: 10,33 кв.см
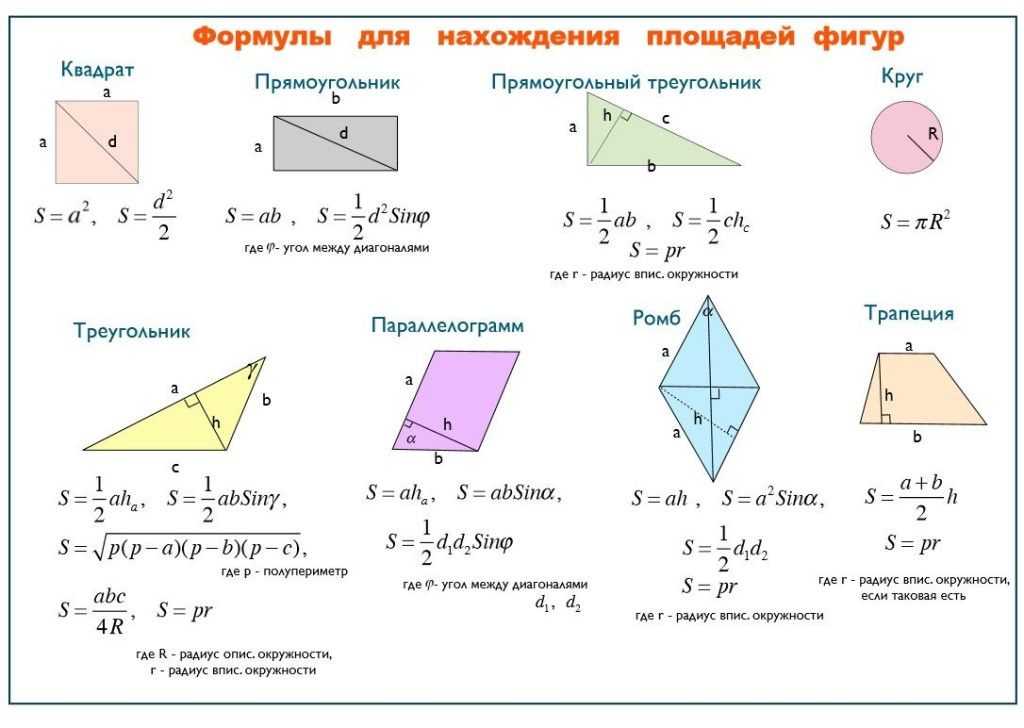
Формулы для четырехугольников
Рассмотрим основные формулы для вычисления площадей различных четырехугольников.
Площадь параллелограмма вычисляется по формуле:
S = a * h
где a - длина стороны, h - высота, опущенная на эту сторону.
Площадь ромба находится как:
S = a * a * sin α
где a - сторона ромба, α - угол между сторонами.
Для трапеции используется формула:
S = (a + b) * h / 2
где a и b - основания трапеции, h - высота.
| Фигура | Формула площади |
| Параллелограмм | S = a * h |
| Ромб | S = a * a * sinα |
| Трапеция | S = (a + b) * h / 2 |
Рассмотрим пример вычисления площади трапеции со сторонами 10 и 6 см и высотой 4 см:
S = (10 + 6) * 4 / 2 = 16 * 4 / 2 = 32 кв.см
Ответ: 32 кв.см
Формулы для круга и частей круга
Площадь круга вычисляется по формуле:
S = π * R^2
где R - радиус круга.
Часто бывает нужно найти площадь не всего круга, а только его части - сектора. Для этого используют формулу:
S = (π * R^2 * α) / 360
где α - центральный угол сектора в градусах.
Например, радиус круга равен 5 см, а центральный угол сектора составляет 60°. Тогда площадь сектора равна:
S = (π * 5^2 * 60) / 360 = 13,09 кв.см

Свойства площадей и их применение
При решении задач на вычисление площадей полезно знать и уметь применять различные свойства площадей. Рассмотрим некоторые из них.
Диагональ прямоугольника делит его на два равных треугольника. Зная площадь прямоугольника, можно легко найти площадь такого треугольника: она равна половине площади прямоугольника.
Это свойство помогает в задачах, когда нужно вычислить площадь нестандартной фигуры. Ее можно разбить на части, площади которых легко найти.
Например, пусть нужно вычислить площадь фигуры, показанной на рисунке. Мы видим, что она состоит из двух прямоугольников. Площадь большого прямоугольника равна 6 * 4 = 24 кв.см. Значит, площадь треугольника равна 24 / 2 = 12 кв.см. Площадь маленького прямоугольника - 3 * 2 = 6 кв.см. Следовательно, общая площадь фигуры равна:
S = 24 + 12 + 6 = 42 кв.см
Подобие фигур и площади
Если две фигуры подобны, то отношение их площадей равно квадрату коэффициента подобия:
S1 / S2 = k^2
Это позволяет находить площадь одной фигуры, зная площадь другой подобной ей.
Например, пусть S1 = 10 кв.см - площадь треугольника. Ему подобен другой треугольник, у которого все стороны в 3 раза больше. Тогда коэффициент подобия равен 3. Площадь второго треугольника составит:
S2 = S1 * k^2 = 10 * 3^2 = 90 кв.см
Полезные советы и рекомендации
Чтобы легко запомнить основные формулы площадей, рекомендуется составить шпаргалки с формулами и рисунками для каждой фигуры. Такие шпаргалки помогут быстро вспомнить нужную формулу при решении задач.
При решении задач по вычислению площадей сложных фигур полезно визуально или мысленно разбить фигуру на простые части, площади которых легко найти по известным формулам.
Знание формул площадей в геометрии - это необходимый базовый навык для любого человека. Используйте полученные знания в повседневной жизни, строительстве, дизайне, шитье и вязании, оформлении интерьера и ландшафта. Это поможет экономить материалы и финансы.
Применение формул площадей на практике
Знание формул для вычисления площадей геометрических фигур имеет большое практическое значение в самых разных областях. Рассмотрим некоторые примеры.
Строительство и ремонт
При планировании ремонта или строительства здания необходимо точно рассчитать, какое количество материалов потребуется. Например, чтобы уложить напольную плитку или ламинат, нужно знать площадь пола. Для облицовки стен кафельной плиткой надо вычислить их площадь. Аналогично для покраски или оклейки обоями стен и потолков.
Ландшафтный дизайн
При проектировании ландшафта важно правильно рассчитать площади участков под газоны, клумбы, дорожки. Требуемое количество растений, семян травы, удобрений напрямую зависит от площадей посадок. Формулы площадей помогают все точно посчитать.
Дизайн интерьера
Дизайнеры интерьера постоянно вычисляют площади помещений, чтобы правильно подобрать мебель, светильники, бытовую технику, ковры и другие элементы декора. Знание формул упрощает расчет необходимого количества обоев, плитки, линолеума, краски при отделке помещений.
Пошив и вязание одежды
Площади деталей одежды необходимо знать, чтобы рассчитать требуемое количество ткани для пошива. Формулы помогают определить, сколько пряжи потребуется для связанных вещей.
Изготовление мебели
При производстве мебели точный расчет площадей поверхностей позволяет экономно расходовать материалы - древесину, стекло, металл, пластик. Благодаря формулам можно заранее определить объем заготовок для деталей.
Задачи на вычисление площадей
Рассмотрим несколько примеров задач на вычисление площадей различных фигур.
Задача 1
Дан прямоугольный треугольник с катетами 6 и 8 см. Найдите его площадь.
Решение. Площадь прямоугольного треугольника равна половине произведения его катетов:
S = (6 * 8) / 2 = 24 кв.см
Ответ: 24 кв.см
Задача 2
Дана трапеция с основаниями 10 и 18 см и высотой 6 см. Найдите ее площадь.
Решение. По формуле площади трапеции:
S = (10 + 18) * 6 / 2 = 28 * 6 / 2 = 84 кв.см
Ответ: 84 кв.см
Задача 3
Дан сектор круга с радиусом 5 см и центральным углом 120°. Найдите площадь сектора.
Решение. По формуле площади сектора:
S = (π * 5^2 * 120) / 360 = 10π кв.см
Ответ: 10π кв.см
Таким образом, умение вычислять площади геометрических фигур по известным формулам - важнейший математический навык с множеством практических применений.
Похожие статьи
- Знак зодиака Скорпион (мужчина): характеристика и совместимость с другими астрологическими знаками
- Подготовка к исповеди. Список грехов для исповеди
- Мифы Древней Греции: краткое содержание и суть
- К чему снится смерть детей? Сонник: умер ребенок. Толкование снов
- Специальность "Технология машиностроения". Кем можно работать?
- Первопечатник Иван Федоров: биография краткая для детей
- 5 стадий принятия неизбежного. Психология человека
