Что такое наклонная в геометрических задачах? Теоремы и применение

Геометрия - одна из важнейших наук, изучающих пространственные формы и отношения. Понимание геометрических фигур и умение решать задачи помогает развивать логическое мышление и пространственное воображение. В данной статье речь пойдет о таком важном понятии геометрии как "наклонная". Что это такое? Какие бывают виды наклонных? Как применить теоремы о наклонных при решении задач? Ответы на эти и другие вопросы вы найдете далее.

Что такое "наклонная" в геометрии

В геометрии наклонной называют прямую линию или поверхность, которая отклоняется от вертикального или горизонтального положения. Наклонная может быть наклонена вправо или влево, вниз или вверх, но всегда отклоняется от горизонтали или вертикали.

Наклонная линия - это линия, идущая под углом к горизонтальной плоскости. Она может быть прямой или кривой.

Наклонная плоскость - плоскость, отклоненная от горизонтального или вертикального положения. Пример - скат крыши.

Наклонный отрезок - отрезок прямой линии, наклоненный под углом к горизонтальной прямой. Например, ступенька лестницы.

Примеры наклонных:

• Лестница
• Скат крыши
• Пандус
• Линия тренда на графике
• Горка

Основные свойства наклонной:

• Длина
• Угол наклона к горизонтальной плоскости
• Положение относительно других линий и фигур

Наклонные бывают:

1. Прямые и кривые
2. С положительным и отрицательным углом наклона

Наклонная отличается от:

• Перпендикуляра - перпендикуляр всегда под прямым углом
• Параллельных линий - параллельные линии не пересекаются и сохраняют постоянное расстояние

Итак, наклонная - это линия или плоскость в геометрии, которая отклоняется от вертикали или горизонтали. Знание свойств наклонных помогает решать многие геометрические задачи.

Теоремы о наклонных и их применение

Теорема о проекции наклонной

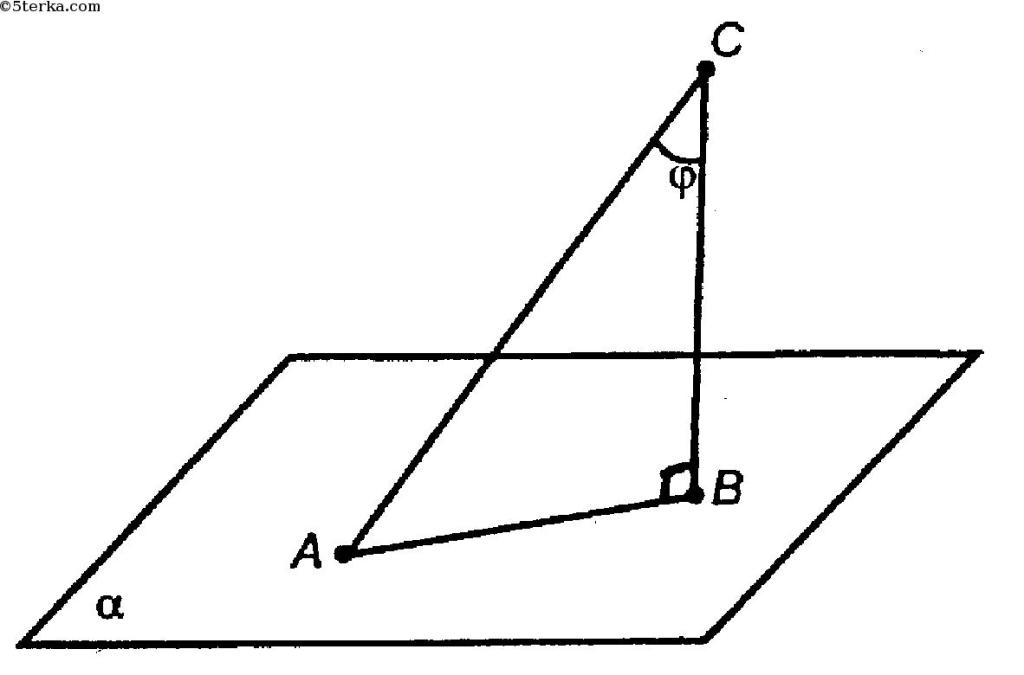
Если из одной точки проведены перпендикуляр и наклонная к плоскости, то отрезок между основаниями перпендикуляра и наклонной называется проекцией наклонной на эту плоскость.

Из рисунка видно, что АВ - перпендикуляр, АС - наклонная, ВС - проекция наклонной АС на плоскость α.

Эта теорема используется при нахождении проекции наклонной на плоскость в задачах. Например:

В треугольнике ABC проведена наклонная АМ. Найдите проекцию наклонной AM на сторону BC, если AB = 5 см, BC = 6 см.

Решение: Проводим перпендикуляр AM. Тогда ВМ - искомая проекция наклонной AM на сторону BC. По теореме Пифагора: AM^2 = AB^2 + BM^2 AM^2 = 25 + BM^2 BM = sqrt(AM^2 - 25) BM = 4 см

Теорема о трех перпендикулярах

Если из точки проведены к плоскости перпендикуляр, наклонная и прямая, проходящая через основание наклонной перпендикулярно проекции наклонной, то эта прямая перпендикулярна самой наклонной.

На рисунке OA ⊥ плоскости α, OC - наклонная, CB ⊥ OC'

По теореме: если CB ⊥ OC', то CB ⊥ OC

Эта теорема используется при доказательстве перпендикулярности прямых в задачах. Например:

Докажите, что медиана CM треугольника ABC перпендикулярна биссектрисе BD.

Решение: Из вершины C опускаем перпендикуляр CH на сторону AB. CM - медиана, CH - ее проекция. BD - биссектриса, проходящая через основание наклонной CM. BD ⊥ CH, как биссектриса треугольника ABC. По теореме о трех перпендикулярах, раз BD ⊥ CH, а CH - проекция наклонной CM, то BD ⊥ CM.