Метод прямоугольников: полное руководство

Метод прямоугольников - простой и наглядный способ приближенного вычисления определенных интегралов. Даже если вы никогда не слышали о нем раньше, это руководство поможет разобраться в сути метода и научит применять его на практике для решения интегральных задач.
Сущность метода прямоугольников
Почему вообще нужно приближенно вычислять интегралы? В некоторых случаях под интегралом стоит сложная функция, для которой невозможно найти точное аналитическое решение. Например, может быть задан график или таблица значений функции, полученная экспериментально.
Тогда на помощь приходит геометрическая интерпретация интеграла как площади под графиком функции. Вместо точного вычисления этой площади мы будем приближенно заменять ее суммой площадей прямоугольников, что дает название всему методу.
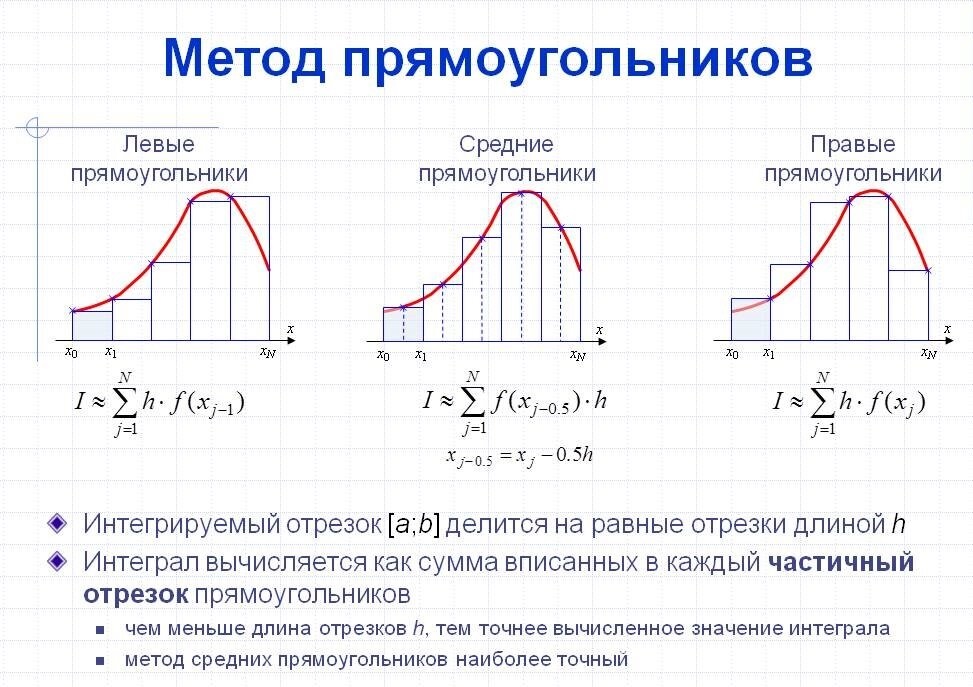
Три разновидности метода прямоугольников
- Метод левых прямоугольников
- Метод правых прямоугольников
- Метод средних прямоугольников
Эти методы отличаются тем, как именно выбирается высота каждого прямоугольника - по левому краю отрезка, по правому или посередине. Далее мы подробно разберем математическое обоснование каждого из них.
Математическое обоснование
Для вывода основных формул метода прямоугольников рассмотрим функцию f(x), заданную на отрезке [a, b]. Разобьем этот отрезок точками x0, x1, ..., xn на n мелких отрезков:
Тогда для метода левых прямоугольников имеем сумму площадей:
а для метода правых прямоугольников:
Формула для метода средних прямоугольников выводится аналогично, с той лишь разницей, что высота каждого прямоугольника выбирается посередине соответствующего отрезка разбиения.
Метод прямоугольников является численным методом для приближенного вычисления определенного интеграла. В этом методе область под графиком функции разбивается на прямоугольники, а значение интеграла приближенно вычисляется как сумма площадей этих прямоугольников.
В зависимости от выбора точки, которая определяет высоту прямоугольника, выделяют три вида метода прямоугольников: левых, правых и средних прямоугольников.

Реализация метода прямоугольников
Для практического вычисления методом прямоугольников нужно выполнить следующие шаги:
- Разбить отрезок интегрирования точками
x0, x1, ..., xnнаnмелких отрезков - Выбрать одну из трех разновидностей метода (левых, правых или средних прямоугольников)
- Построить на каждом отрезке соответствующий прямоугольник и вычислить его площадь
- Просуммировать площади всех прямоугольников, получив приближенное значение исходного интеграла
При этом разбиение отрезка на подынтервалы может быть как равномерным, так и неравномерным. В первом случае все точки делят отрезок на равные части, а во втором - точки выбираются произвольно.
Автоматизация расчетов в Excel
Для упрощения вычислений по приведенным выше формулам удобно использовать электронные таблицы, например MS Excel. Ниже приведен пример реализации метода средних прямоугольников с равномерным разбиением отрезка.
| x | f(x) | Δx | xi | f(xi) | S |
| 0 | 1 | 0.2 | 0.1 | 1.095 | =C3*D4 |
| 0.2 | 1.105 | 0.2 | 0.3 | 1.155 | =C3*D5 |
| 0.4 | 1.225 | 0.2 | 0.5 | 1.23 | =C3*D6 |
| 0.6 | 1.365 | 0.2 | 0.7 | 1.32 | =C3*D7 |
| 0.8 | 1.625 | 0.2 | 0.9 | 1.545 | =C3*D8 |
| 1 | 2 | =SUM(F3:F8) |
Здесь задан шаг разбиения Δx = 0.2, вычислены значения функции в средних точках каждого отрезка и посчитаны площади соответствующих прямоугольников. Их сумма в последней ячейке и есть результат.

Оценка точности результата
Любое приближенное значение интеграла, полученное методом прямоугольников, будет отличаться от точного результата. Это отличие называют погрешностью метода. Для оценки погрешности используют следующие подходы:
- Нахождение верхней границы погрешности по специальной формуле
- Сравнение с результатом при удвоенном количестве отрезков разбиения
- Проверка выполнения критерия заданной точности
Подробнее об этих способах оценки точности мы поговорим в следующих разделах.
Уже сейчас вы можете приступать к практическому применению метода прямоугольников для приближенного вычисления определенных интегралов! В следующих частях статьи вы найдете еще больше полезных советов по использованию этого простого, наглядного и универсального метода.
Оптимизация вычислений
Чтобы сократить время на вычисления методом прямоугольников, можно воспользоваться следующими приемами:
Правило Рунге
Это правило позволяет оценить верхнюю границу погрешности для метода средних прямоугольников, не прибегая к дополнительным вычислениям. Согласно правилу Рунге, погрешность не превосходит величины M(b-a)^3/24n^2, где M - максимальное значение второй производной функции на заданном отрезке.
Методы высших порядков точности
Существуют обобщения метода прямоугольников - методы Ньютона-Котеса более высоких порядков. Они используют для аппроксимации не прямоугольники, а более сложные фигуры, что позволяет получить более точный результат при том же количестве отрезков разбиения.
Компьютерная реализация
Для сложных функций и большого количества подынтервалов удобно реализовывать метод прямоугольников на компьютере. Это позволит быстро пересчитывать приближение при изменении параметров (числа отрезков, точности и т.п.).
Примеры применения метода
Рассмотрим несколько конкретных примеров использования метода прямоугольников для вычисления определенных интегралов. В качестве интегрируемой функции возьмем f(x) = 2x + sin(x) на отрезке от 0 до π.
Задача 1
Вычислить интеграл с 5 отрезками разбиения методом средних прямоугольников.
Задача 2
Вычислить интеграл с точностью 0.05. Сравнить результаты для 10 и 20 отрезков.
Задача 3
Вычислить интеграл методом трапеций и методом правых прямоугольников с 15 отрезками. Сравнить точность.
Границы применимости метода
Хотя метод прямоугольников достаточно универсален, у него есть некоторые ограничения:
Требования к интегрируемой функции
Функция должна быть непрерывной на заданном отрезке интегрирования. Также желательно, чтобы она была дифференцируема, тогда можно оценить погрешность.
Сходимость приближения
По мере увеличения количества отрезков разбиения результат обязан сходиться к точному значению интеграла. Если этого не происходит - something's wrong.
Сравнение с другими методами
При одинаковой точности метод прямоугольников требует большего количества отрезков, чем, например, метод трапеций или метод Симпсона. Поэтому для сложных интегралов он зачастую уступает в скорости.
Похожие статьи
- Птица ударилась в окно: что означает примета? Птица ударилась в окно - к чему это?
- И. Бунин "Одиночество": анализ стихотворения по плану
- Гуманитарные профессии. Профессии социально-гуманитарного профиля
- Как хоронят мусульманина. Мусульманский обряд похорон
- Чем отличается университет от института? Институт и университет: в чем разница
- Где находятся мощи Спиридона Тримифунтского? Феномен нетленных мощей Спиридона Тримифунтского
- История развития вычислительной техники. Отечественная вычислительная техника. Первая ЭВМ
