Сечение плоскостью цилиндра: геометрия пространства

Геометрия пространства полна загадок. Одной из самых интересных является вопрос: как выглядит сечение цилиндрической поверхности произвольной плоскостью? Давайте разберемся!

Основные понятия

Цилиндр — это поверхность, образованная прямыми линиями, параллельными данному направлению, которые пересекают две заданные кривые. Элементы цилиндра: ось, образующие, основания.

Плоскость может располагаться по отношению к цилиндру перпендикулярно его оси, под наклоном или параллельно образующим.

Под сечением понимают пересечение какой-либо поверхности с плоскостью.

Виды сечений цилиндра плоскостью:

• Окружность
• Эллипс
• Две пересекающиеся прямые

Рассмотрим подробнее каждый из этих случаев.

Сечение плоскостью, перпендикулярной оси цилиндра

Если плоскость расположена перпендикулярно оси цилиндра, то линия пересечения имеет форму окружности, параллельной основанию цилиндра. Это можно строго доказать, используя свойства параллельного переноса.

Теорема: Плоскость, перпендикулярная оси цилиндра, пересекает его по окружности, параллельной основанию.

На практике такое перпендикулярное сечение часто используется, например, при нарезании цилиндрических заготовок заданной толщины.

Для наглядности приведем иллюстрацию:

Как видно из рисунка, получается аккуратная окружность, равная основанию цилиндра.

Сечение наклонной плоскостью

Еще один распространенный случай — сечение цилиндрической поверхности наклонной плоскостью. Здесь линия пересечения представляет собой эллипс.

Теорема: Плоскость, наклоненная под произвольным углом к оси цилиндра, пересекает его по эллипсу.

Для вычисления площади такого эллиптического сечения используется формула:

где a и b — полуоси эллипса.

Площадь сечения цилиндра плоскостью и построение проекций эллипса

При решении задач на пересечение цилиндра наклонной плоскостью важно уметь корректно строить проекции получающегося эллипса. Рассмотрим основные моменты:

1. Определяем фронтальную проекцию одной пары точек пересечения
2. Находим их горизонтальную проекцию
3. Строим профильную проекцию с учетом видимости
4. Обозначаем соответствующие размеры на проекциях

Так пошагово можно получить проекции искомого эллипса.

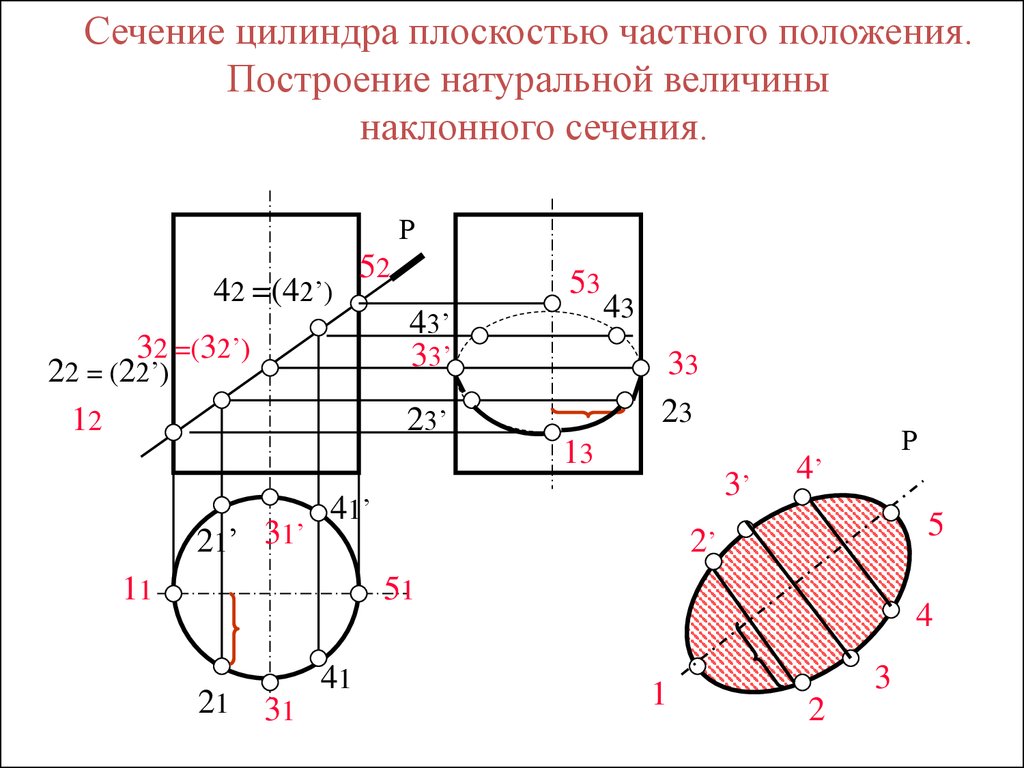
Линия пересечения плоскости с цилиндрической поверхностью - это овал, полученный путем сжатия или растяжения окружности, в математике такая поверхность называется эллипсом. Эллипс имеет центр симметрии и две взаимно перпендикулярные оси симметрии. Отрезки этих осей симметрии, заключенные внутри эллипса, называются большой и малой осями эллипса.

Построение натуральной величины сечения

Для наглядности и возможности вычислений также важно уметь строить натуральный вид сечения цилиндра. Это можно сделать, например, методом совмещения плоскости с горизонтальной плоскостью проекций или указанием координат ряда точек эллипса.

Построение развертки цилиндра

Рассмотрим пример развертки боковой поверхности цилиндра с эллиптическим сечением (см. рисунок). Здесь длина основания заменена периметром вписанного многоугольника, через точки деления проведены образующие, на которых отмечены точки пересечения с

Таким образом получается развертка боковой поверхности цилиндра с отмеченной на ней линией пересечения секущей плоскостью. Это позволяет наглядно увидеть форму сечения и использовать развертку для дальнейших расчетов.

Сечение плоскостью, параллельной образующим

В сечении сферы плоскостью всегда образуется окружность, которая может проецироваться в виде отрезка прямой, в виде эллипса или в виде окружно-

Еще один частный случай — когда секущая плоскость расположена параллельно образующим цилиндра. Здесь линия пересечения представляет собой две пересекающиеся прямые. Эти прямые являются параллельными хордами оснований цилиндра.

На практике такое сечение может использоваться, к примеру, при раскрое листового материала.

Осевое сечение цилиндра

Особым случаем сечения плоскостью, параллельной образующим цилиндра, является осевое сечение. Здесь секущая плоскость проходит непосредственно через ось цилиндра.

Линия пересечения при осевом сечении представляет собой квадрат, сторона которого равна диаметру основания цилиндра. Используя это, можно вычислить площадь основания цилиндра, зная площадь его осевого сечения.