Параметрически заданная функция: свойства и особенности

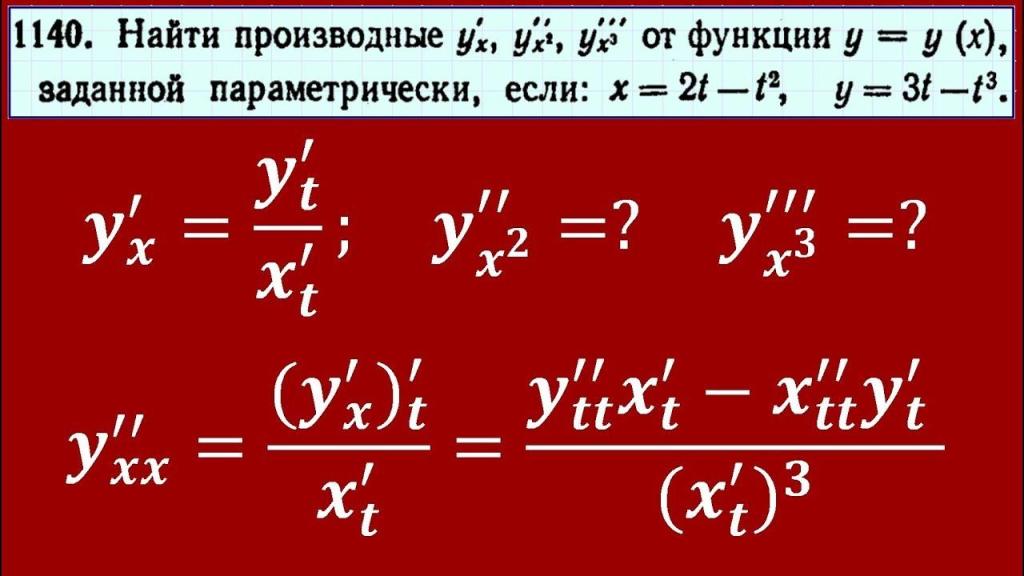
Параметрически заданные функции представляют собой особый класс математических объектов, который позволяет моделировать гораздо более широкий спектр функциональных зависимостей по сравнению с обычными функциями одной переменной. В данной статье мы разберем, что такое параметрически заданные функции, чем они отличаются от привычных функций, как строить их графики и находить производные.

Определение параметрически заданной функции

Формально, параметрически заданной называется функция вида:

• x = x(t)
• y = y(t)

Здесь t - некоторый параметр. Отличие от обычного определения функции y(x) состоит в том, что x тоже является функцией от t. Это позволяет задавать гораздо более широкий класс функциональных зависимостей.

Примеры параметрически заданных функций

Рассмотрим несколько примеров параметрического задания различных функций:

• Окружность радиуса R с центром в начале координат: x(t) = R*cos(t) y(t) = R*sin(t)
• Эллипс с полуосями a и b: x(t) = a*cos(t) y(t) = b*sin(t)
• Парабола: x(t) = t y(t) = t²

Графическая интерпретация параметрически заданных функций

Каждая пара x(t), y(t) задает точку на координатной плоскости. При изменении параметра t от t_min до t_max мы получаем набор точек, которые формируют график функции.

Например, для окружности при t изменяющемся от 0 до 2π точки образуют замкнутую кривую - окружность. А для параболы при t от -∞ до +∞ точки формируют незамкнутую кривую.

Область определения и область значений

Областью определения параметрически заданной функции является множество значений параметра t. А областью значений - множество всех пар x(t) и y(t) при t из области определения.

Например, для рассмотренной выше параболы область определения - вся числовая прямая (-∞; +∞), а область значений - множество точек на самой параболе.

Представление параметрической функции в явном виде

Как уже отмечалось ранее, для некоторых простых случаев возможен переход от параметрического задания функции к явной зависимости y(x).

Однако для многих функций такое представление оказывается невозможным в элементарных функциях или громоздким. Поэтому работать приходится непосредственно с параметрически заданной формой.

Нахождение производной функции заданной параметрически

Для вычисления производной параметрической функции используется формула:

y′(t) = dy/dt / dx/dt

Где dy/dt и dx/dt - производные функций y(t) и x(t) по параметру t.

Применение параметрического задания функций на практике

Параметрические функции широко используются в различных областях:

• Механика - описание движения тел
• Физика - описание физических процессов
• Экономика - моделирование экономической динамики

Достоинствами такого подхода являются гибкость и универсальность по сравнению с классическим заданием функции y(x).

Преимущества параметрического задания функций

К основным преимуществам параметрического задания функций по сравнению с явным видом можно отнести:

1. Возможность описания более широкого класса функциональных зависимостей, в том числе неявных и сложных
2. Простота задания и изучения свойств таких объектов как окружность, эллипс, парабола и др.
3. Удобство применения в физических и других прикладных задачах, где естественным образом возникает параметр (например, время)
4. Наглядность и простота построения графиков
5. Возможность непрерывного перехода вдоль линии или поверхности при изменении параметра

Недостатки и ограничения параметрического подхода

При всех достоинствах у параметрического способа задания функций есть и определенные недостатки:

• Громоздкость записи по сравнению с явным видом y(x) для простых функций
• Бо́льшая сложность преобразований и вычислений по сравнению с элементарными функциями
• Проблема выбора подходящего параметра и диапазона его изменения
  

Задание функций другими способами

Помимо явного и параметрического заданий, функции могут быть описаны:

• Неявно - например, уравнением вида F(x, y) = 0
• Таблично - наборами значений аргумента и функции
• Графически - в виде готового графика функции

Выбор оптимального способа задания функции

При решении конкретной задачи важно выбрать наиболее подходящий способ задания функций. Это зависит от целей исследования, требуемых вычислений, необходимости изучения свойств функции и других факторов.

Во многих случаях параметрическое задание дает оптимальный баланс гибкости, простоты и наглядности.

Комбинированное задание функций

На практике часто используется комбинированное задание функций - с применением разных способов для разных участков области определения или области значений.

Например, кусочно-заданная функция может быть описана аналитически на одном участке и таблично - на другом. А параметрически могут быть заданы отдельные части графика функции нескольких переменных.

Параметрическое vs параметризованное задание

Стоит отличать параметрически заданные функции от параметризованных семейств функций. В последнем случае мы фиксируем некоторый параметр и рассматриваем семейство функций от одной переменной.

Например, распределения с параметром формы k или полиномы степени n. Здесь параметр не является аргументом функции.

Обратные параметрические функции

Если задана функция в параметрическом виде x(t), y(t), то обратная функция будет иметь вид t(x,y). Геометрически это соответствует переходу от исходной кривой к кривой, обратной по отношению к ней.

Аналитически нахождение такой обратной функции может быть весьма сложной задачей даже для простых случаев.

Обобщение на многомерный случай

Параметрический подход можно обобщить и на случай функций нескольких переменных z = f(x,y). Здесь в роли параметра могут выступать дополнительные переменные t, p, q.

Это особенно удобно при моделировании поверхностей и гиперповерхностей в многомерных пространствах.