Дизъюнкция - это логическая операция, объединяющая высказывания: определение, свойства, применение
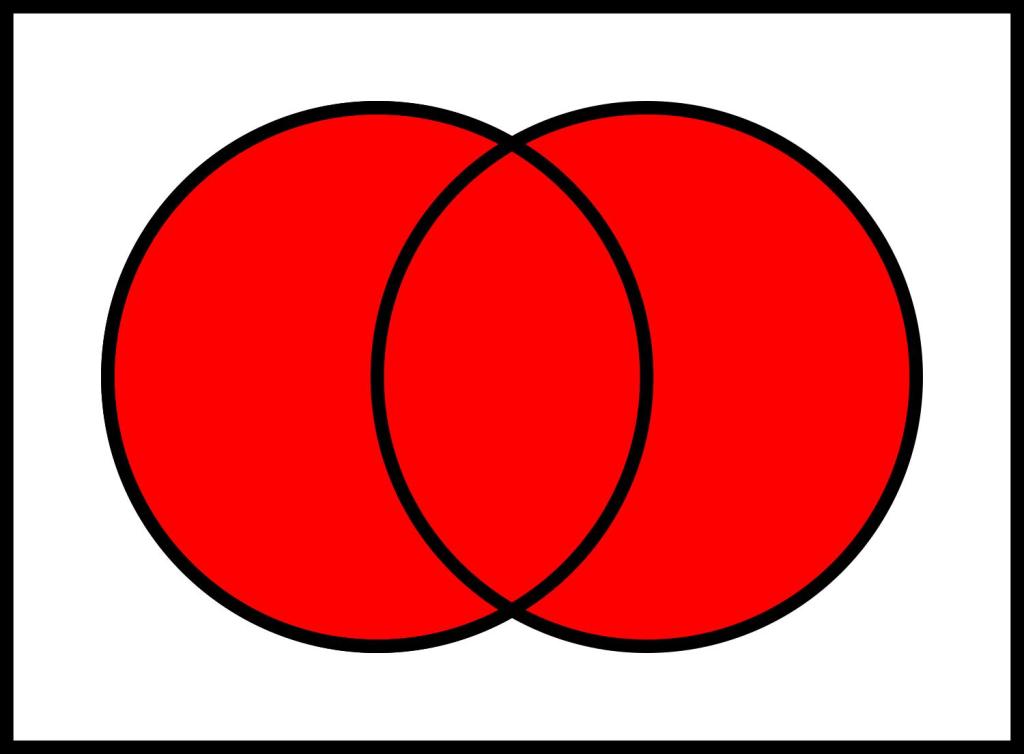
Дизъюнкция является одной из фундаментальных логических операций, широко используемых в математической логике, программировании, лингвистике и других областях. Она позволяет объединять несколько высказываний в одно сложное высказывание на основе принципа "или". Давайте подробно разберем, что из себя представляет дизъюнкция.
Определение дизъюнкции
Формально дизъюнкция определяется как логическая операция, которая принимает на вход два или более высказывания и возвращает значение "истина", если хотя бы одно из входных высказываний является истинным.
Дизъюнкцией высказываний A и B называется высказывание C, которое принимает значение "ложь" только в том случае, когда оба высказывания A и B ложны.
В естественном языке дизъюнкции соответствует смысловое значение союза "или". Например, высказывания "Сегодня идет дождь" и "Сегодня светит солнце" можно объединить дизъюнкцией: "Сегодня идет дождь или светит солнце".
Обозначение дизъюнкции
В математической логике для дизъюнкции используются различные обозначения, наиболее распространенные:
- ∨ (вертикальная черта)
- + (знак плюс)
- V (заглавная буква V)
- || (две вертикальные черты)
Например, дизъюнкция высказываний A и B может быть записана как A ∨ B, A + B, A V B, A || B.
В языках программирования традиционно используются обозначения | для побитовой дизъюнкции и || для логической дизъюнкции.
Свойства дизъюнкции
Как и другие логические операции, дизъюнкция обладает рядом свойств, которые полезно знать при ее использовании.
Коммутативность
Порядок следования высказываний в дизъюнкции не имеет значения:
A ∨ B ≡ B ∨ A
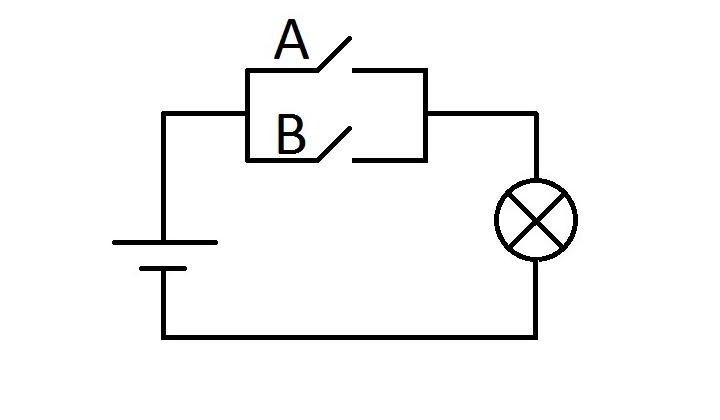
Ассоциативность
Порядок объединения трех и более высказываний не влияет на результат:
(A ∨ B) ∨ C ≡ A ∨ (B ∨ C)
Дистрибутивность
Дизъюнкция распределяется через конъюнкцию:
A ∨ (B ∧ C) ≡ (A ∨ B) ∧ (A ∨ C)
Это очень полезное свойство, позволяющее упростить многие логические выражения.
| A | B | A ∨ B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
В таблице приведена таблица истинности для дизъюнкции двух высказываний (A и B). Видно, что дизъюнкция принимает значение "ложь" только в одном случае, когда оба высказывания ложны (0 и 0).
Дизъюнкция: отличительные свойства
Формально дизъюнкция является одной из базовых логических операций, наряду с конъюнкцией, импликацией, отрицанием. Эти операции составляют фундамент математической логики и широко используются для формализации высказываний и построения логических выражений.
Ключевое отличие дизъюнкции как логической операции заключается в том, что она объединяет несколько высказываний по принципу "или", в отличие от конъюнкции ("и") и других операций. Это позволяет строить гибкие логические конструкции.
Например, с помощью дизъюнкции можно формализовать такие высказывания:
- "Данное число делится на 2 или на 5"
- "Погода сегодня дождливая или облачная"
- "Фигура является квадратом или прямоугольником"
В математической логике и дискретной математике дизъюнкция играет ключевую роль, являясь базовой операцией для формирования сложных логических выражений и предикатов.

Суть дизъюнкции
По своей сути дизъюнкция представляет собой операцию объединения высказываний по принципу "или". Она позволяет комбинировать два и более простых высказывания в одно сложное высказывание.
Например, имея высказывания:
- A: "Сегодня идет дождь"
- B: "Сегодня светит солнце"
Можно объединить их при помощи дизъюнкции:
A ∨ B: "Сегодня идет дождь или светит солнце"
Полученное высказывание будет истинным, если хотя бы одно из исходных высказываний A или B является истинным. Так достигается эффект объединения высказываний.
Аналогично дизъюнкция позволяет объединять события, условия, ограничения:
- "Доступ разрешен пользователям группы А или группы B"
- "Платеж принимается в долларах США или евро"
Таким образом, дизъюнкция является важнейшим инструментом для объединения различных высказываний и условий в формализованных системах.
Применение дизъюнкции в математической логике
В математической логике дизъюнкция широко используется для формализации математических утверждений и доказательств. Она позволяет гибко формулировать условия истинности сложных высказываний через объединение более простых высказываний.
Например, теорему о том, что "данное число делится на 6 тогда и только тогда, когда оно делится на 2 или на 3" можно записать с использованием дизъюнкции:
(A делится на 6) ⇔ ((A делится на 2) ∨ (A делится на 3))
Здесь дизъюнкция позволяет объединить два альтернативных условия делимости числа.
Дизъюнкция в теории алгоритмов
В теории алгоритмов и программировании дизъюнкция часто используется для описания ветвлений в логике работы программы или алгоритма. Например:
if (условие1) или (условие2): выполнить действие
Здесь дизъюнкция условий позволяет выполнить действие, если выполнено хотя бы одно из условий.
Дизъюнкция в лингвистике
В лингвистике и логике естественного языка дизъюнкция соответствует использованию разделительных союзов "или", "либо" для объединения смысловых конструкций и утверждений. Например:
"Он поедет в отпуск либо в июне, либо в июле"
Здесь дизъюнктивная конструкция позволяет объединить два варианта события.
Дизъюнкция в языках программирования
В языках программирования реализованы специальные логические операции для описания дизъюнкции в программном коде. Чаще всего используются:
- OR в языках Pascal, Ada
- || в языках C, C++, Java, JavaScript
- or в Python
Эти операции позволяют гибко управлять логикой выполнения программы на основе объединения различных условий, например:
if (x > 5 || y < 10) { // выполнить действие } Здесь дизъюнкция двух условий управляет входом в ветвление программы.
Реализация строгой дизъюнкции
В некоторых языках также поддерживается операция "исключающего ИЛИ" или строгой дизъюнкции, которая возвращает истину только при одном истинном операнде. Например, в Python это оператор ^:
x = 1 y = 2 print(x ^ y) # True Такая форма дизъюнкции полезна для различения взаимоисключающих случаев и событий в программах.
Применение дизъюнкции на практике
Помимо формальных систем, дизъюнкция широко применяется в повседневной жизни, политике, экономике, юриспруденции и других областях для формулировки альтернатив или объединения условий. Рассмотрим несколько практических примеров.
Похожие статьи
- Устное народное творчество: виды, жанры произведений и примеры
- Практическое значение биологии в жизни человека, в медицине, в пищевой промышленности
- Примеры текстов разговорного стиля речи. Понятие и признаки разговорной речи
- Что изучает история? Зачем нужно изучать историю? История мира
- Где находятся мощи Спиридона Тримифунтского? Феномен нетленных мощей Спиридона Тримифунтского
- Характеристика Льва-женщины. Знак Зодиака Лев: описание
- История Кёсем Султан: биография, правление и интересные факты
