Вычисление высоты правильного треугольника - простая формула

Знаете ли вы, что в правильном треугольнике все три высоты полностью совпадают с медианами и биссектрисами? Этот удивительный факт делает вычисление высоты очень простым. Высота - ключ к решению многих задач на правильный треугольник. Я научу вас с легкостью находить этот важный элемент, используя всего лишь сторону треугольника. Овладейте мощным инструментом - формулой высоты правильного треугольника!

Основные свойства правильного треугольника
Правильный треугольник - это треугольник, у которого все три стороны и все три угла равны. Длина каждой стороны обозначается буквой a. Каждый угол равен 60 градусам. Это вытекает из свойств суммы углов треугольника, которая всегда равна 180 градусам.
Из равенства всех сторон правильного треугольника следует простая формула периметра:
P = 3*a
Площадь правильного треугольника со стороной a вычисляется по формуле:
S = (a2*√3)/4
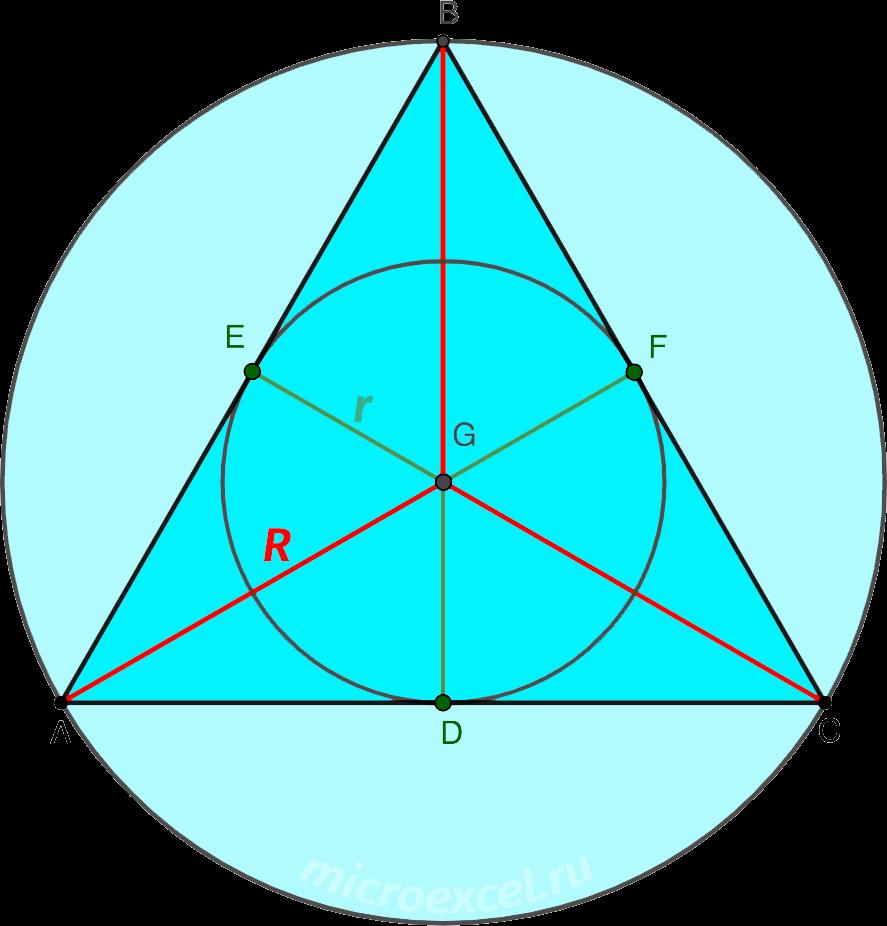
В правильном треугольнике можно вписать окружность, касающуюся всех его сторон, и описать вокруг него окружность, проходящую через все вершины.
Центр вписанной окружности совпадает с центром описанной окружности и является общим центром симметрии всего правильного треугольника.
- Медианы делятся центром в отношении 2:1
- Биссектрисы и высоты проходят через центр
- Серединные перпендикуляры также проходят через центр
Вывод формулы высоты правильного треугольника
Найдем высота правильного треугольника тремя способами: с помощью теоремы Пифагора, формулы площади и тригонометрических функций.
Рассмотрим прямоугольный треугольник, образованный высотой правильного треугольника:
| Катет | a |
| Гипотенуза | a |
| Высота (искомая) | h |
Применим теорему Пифагора:
a2 = h2 + (a/2)2
Отсюда: высота правильного треугольника равна a*√3/2
Аналогичный результат получим, приравняв площади треугольников. Третий способ - через тригонометрическое отношение sin60°=√3/2.
Итак, мы вывели одну и ту же формулу тремя способами:
- Через теорему Пифагора
- Через формулу площади
- Через тригонометрические функции
Примеры задач на вычисление высоты
Рассмотрим несколько примеров, как можно использовать полученную формулу в задачах на вычисление высоты правильного треугольника.
Задача 1. Дана сторона, найти высоту
Длина стороны правильного треугольника равна 10 см. Требуется найти длину высоты. Решение: подставляем значения в формулу высоты h = a*√3/2.
h = 10*√3/2 = 8,66 см
Ответ: высота равна 8,66 см.
Задача 2. Через радиус описанной окружности
Дан правильный треугольник, радиус его описанной окружности равен R. Найти высоту треугольника, если известно, что она равна трем радиусам вписанной окружности и в полтора раза меньше радиуса описанной.
Решение:
h = 3r
R = 1,5h
Отсюда: h = 2R/3
Ответ: высота равна 2R/3.
Задача 3. Через радиус вписанной окружности
Дан правильный треугольник со стороной 10 см. Радиус вписанной в него окружности равен 4 см. Найти высоту треугольника, зная, что она в полтора раза больше радиуса вписанной окружности.
Решение:
h = 1,5r
r = 4 см
h = 1,5 * 4 = 6 см
Ответ: высота равна 6 см.
Рекомендации по решению задач на высоту

Анализ условия
Прежде чем подставлять значения в формулы, внимательно изучите условие задачи, выпишите все известные и неизвестные величины.
Выбор формулы
В зависимости от того, какие данные присутствуют в условии, выберите соответствующую формулу для вычислений.
Проверка ответа
Подставьте полученный ответ обратно в условие задачи, убедитесь, что все сходится.
Похожие статьи
- Как узнать свое тотемное животное по дате рождения
- Парные и непарные, звонкие и глухие, мягкие и твердые согласные звуки в русском языке
- Как хоронят мусульманина. Мусульманский обряд похорон
- Расположение органов у человека (фото). Внутренние органы человека: схема расположения
- Где живет слепая ясновидящая баба Нина: адрес и отзывы
- Институты ФСБ России, порядок приема
- История развития вычислительной техники. Отечественная вычислительная техника. Первая ЭВМ
