Свойства пределов функции: базовые понятия, свойства, применение

Пределы функций - одна из фундаментальных концепций математического анализа, позволяющая описывать поведение функции в окрестности заданной точки. Хотя на первый взгляд это может показаться довольно абстрактным и формальным определением, на самом деле за ним скрываются удивительные и полезные свойства, которые часто неожиданным образом проявляются на практике.

Базовые понятия теории пределов функций

Для начала давайте разберемся с основными определениями.

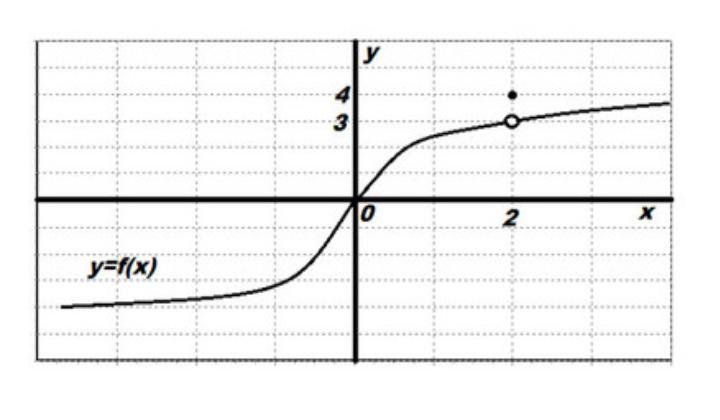
Предел функции f(x) в точке a равен числу L, если значение функции f(x) может быть сколь угодно близко к L при достаточно малых положительных и отрицательных отклонениях аргумента x от точки a.

Геометрически это можно представить так: мы как бы «приближаем» график функции к горизонтальной прямой y = L, варьируя значение x в окрестности точки a. Если график функции при этом может сколь угодно плотно «прилипнуть» к прямой y = L, не пересекая ее, то говорят, что функция имеет предел L при x, стремящемся к a.

Найти предел функции можно несколькими способами:

• подставить предельное значение аргумента a в функцию f(x), если это возможно
• воспользоваться известными свойствами пределов
• перейти к пределу последовательности или ряда, если функция задана таким образом

Знание пределов функций применяется во многих областях математического анализа: при исследовании функций на непрерывность, при вычислении производных и интегралов, в теории рядов, дифференциальных уравнениях и т.д. Так что это важная и фундаментальная концепция!

Основные свойства пределов

Помимо прямого вычисления, пределы функций обладают рядом удивительных свойств, которые часто упрощают работу с ними.

Арифметические свойства пределов

Одним из важнейших свойств пределов являются так называемые арифметические свойства. Они позволяют выносить арифметические операции (сложение, вычитание, умножение, деление) за знак предела:

• Если функции f(x) и g(x) имеют конечные пределы при x, стремящемся к a, то и их сумма (или разность) будет иметь предел, равный сумме (или разности) пределов этих функций.
• То же самое справедливо для произведения и частного функций (при ненулевом пределе знаменателя).

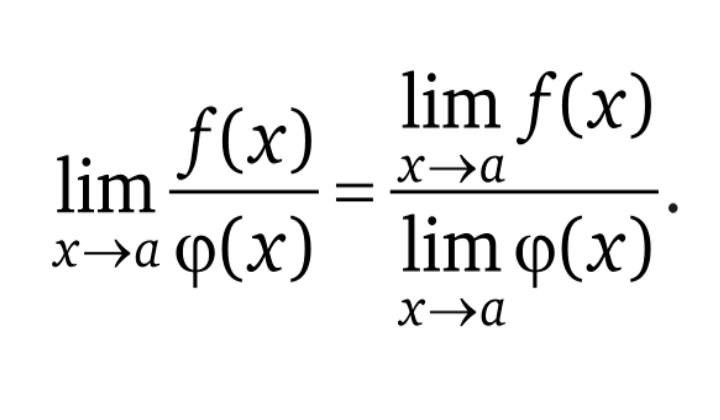
Эти свойства часто используются для упрощения вычислений и «раскрытия» сложных пределов.

Пределы монотонных функций

Еще одним полезным свойством обладают монотонные функции - функции, значения которых либо возрастают, либо убывают. Для таких функций также выполняются интересные закономерности.

Первый и второй замечательные пределы

В математическом анализе выделяют два наиболее часто используемых предела - первый и второй замечательные пределы. Они также демонстрируют любопытные свойства некоторых функций при стремлении аргумента к бесконечности или нулю.

Следствия основных свойств пределов

Из перечисленных выше свойств пределов можно получить множество интересных следствий и результатов, которые упрощают работу с пределами на практике.

Применение свойств пределов функций

Знание свойств пределов широко используется в различных областях:

• При доказательстве непрерывности функций
• В дифференциальном и интегральном исчислении
• В теории рядов и последовательностей
• И так далее

Это лишь несколько примеров из обширного списка возможных применений свойств пределов на практике.

Бесконечно малые и бесконечно большие функции

Еще одним важным понятием, тесно связанным со свойствами пределов, являются бесконечно малые и бесконечно большие функции.

Бесконечно малая функция - это функция, предел которой при стремлении аргумента к некоторому значению равен нулю. А бесконечно большая функция имеет предел, равный бесконечности.

Эти два класса функций также демонстрируют любопытные свойства:

• Произведение бесконечно малой и ограниченной функций также является бесконечно малой
• Частное бесконечно большой и бесконечно малой функций может иметь вполне конечный предел

Примеры бесконечно малых и бесконечно больших функций

К классическим примерам относятся:

• Функция 1/x является бесконечно большой при x, стремящемся к нулю
• Функция sin(1/x) будет бесконечно малой в этом же случае
• Многочлен при стремлении аргумента к бесконечности часто является бесконечно большой или бесконечно малой функцией

С помощью этих примеров можно проиллюстрировать свойства таких функций.

Вычисление бесконечно малых и бесконечно больших частей функций

Для вычисления пределов часто нужно выделить бесконечно большую или бесконечно малую часть исходной функции. Это можно сделать с помощью разложения на множители или применения некоторых алгебраических преобразований.