Тангенс угла. Значения тангенса

Тангенс угла - одна из основных тригонометрических функций, широко используемая в математике, физике, инженерных расчетах и других областях. Рассмотрим подробнее, что такое тангенс угла, его основные свойства и применение.

Определение тангенса угла

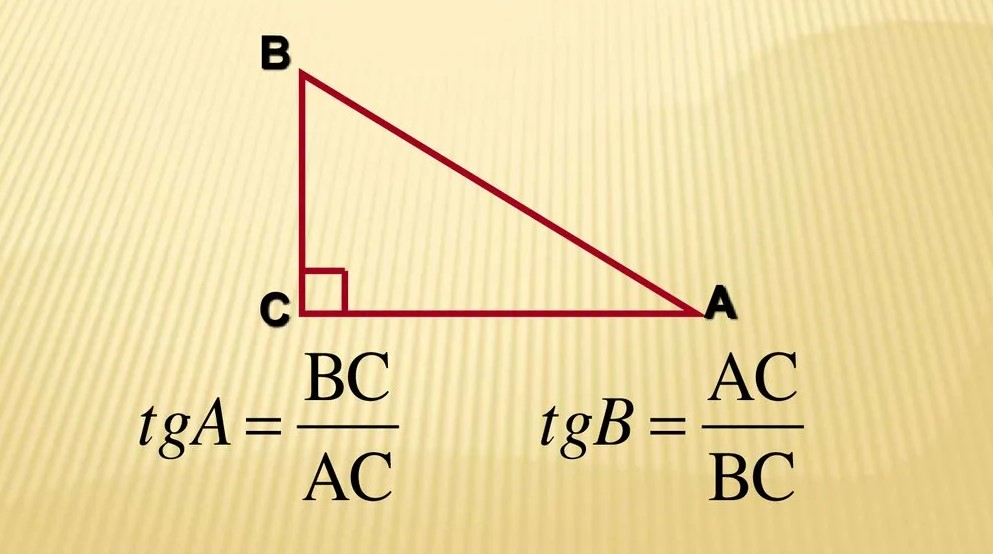
Дадим определение тангенса для острого угла в прямоугольном треугольнике. Пусть дан треугольник ABC с прямым углом C (рис. 1). Тогда тангенс угла A определяется по формуле:

Рис. 1. Вывод формулы тангенса

tg A = BC/AC

где BC - противолежащий катет, AC - прилежащий катет. Иными словами, тангенс угла равен отношению длины противолежащего катета к длине прилежащего.

Связь тангенса с другими тригонометрическими функциями

Кроме определения через катеты, тангенс можно выразить через синус и косинус:

tg A = sin A / cos A

Эта формула часто используется для нахождения тангенса угла, если известны его синус и косинус. Например, при решении различных тригонометрических уравнений и неравенств.

Значения тангенса основных углов

Рассмотрим значения тангенса для некоторых основных и часто встречающихся углов (в градусах):

• tg 0° = 0
• tg 30° = 1/√3
• tg 45° = 1
• tg 60° = √3
• tg 90° - не определен

Полный список значений тангенсов углов от 0° до 360° приведен в тригонометрических таблицах. Зная значение тангенса какого-либо угла, можно определить синус, косинус и другие функции этого угла.

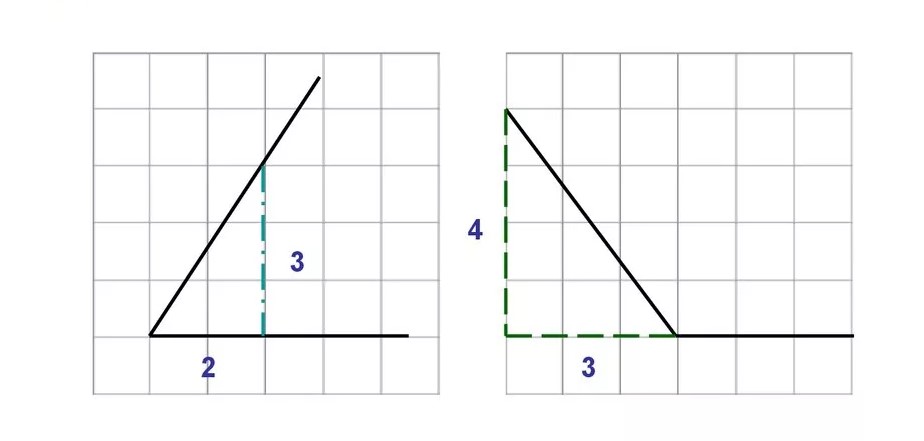
График функции тангенс

Графиком функции y = tg x в декартовой системе координат является периодическая функция с периодом 180° (π радиан). Основные свойства графика:

• Тангенс не определен при х = 90° + 180°k и 270° + 180°k, где k - целое число. В этих точках график разрывный.
• В интервалах (90° + 180°k, 270° + 180°k) тангенс принимает любые значения от -∞ до +∞. График асимптотически приближается к оси OX.

Применение тангенса

Тангенс угла широко используется в различных областях:

1. Решение прямоугольных треугольников - для нахождения неизвестных элементов (углов, сторон) по известным данным.
2. Решение тригонометрических уравнений и неравенств.
3. В инженерных и физических расчетах, требующих знания тригонометрии.
4. При работе с периодическими и гармоническими функциями в математике и физике.
5. В теории волн для описания свойств волн различной природы.

Таким образом, знание тангенса и умение им пользоваться важно во многих математических и прикладных задачах.

Вычисление тангенса угла

Рассмотрим, как вычислить значение тангенса для заданного угла. Существует несколько способов:

1. Использовать таблицу значений тригонометрических функций. В ней для основных углов (0°, 30°, 45°, 60° и т.д.) приведены значения tg.
2. Вычислить tg по формуле через sin и cos: tg α = sin α / cos α. Для этого нужно знать или найти sin и cos данного угла.
3. Построить треугольник с нужным углом, измерить длины катетов и вычислить отношение одного катета к другому.

На практике чаще всего используют первые два способа, так как они не требуют построений и измерений.

Задачи с использованием тангенса

Рассмотрим применение тангенса на примере решения задач:

• Задачи на нахождение углов и сторон в прямоугольном треугольнике.
• Тригонометрические уравнения, содержащие tg.
• Доказательство тригонометрических тождеств, формул.

При решении таких задач нужно уметь находить тангенс по известным данным, а также применять основные тригонометрические формулы преобразования выражений, содержащих tg.

Свойства функции тангенс

К основным свойствам функции y = tg x относят:

• Тангенс - периодическая функция с периодом π.
• Неопределенность (разрывы) при x = π/2 + kπ, где k - целое число.
• Симметричность относительно начала координат: tg(-x) = -tg(x).

Эти свойства следуют из геометрического определения тангенса и вида его графика. Их нужно учитывать при исследовании функции, решении уравнений и неравенств.

Практические приложения

Кроме «чисто» математических задач, тангенс находит множество применений в физике и технике. Например:

• Описание гармонических колебаний с помощью тригонометрических функций, в том числе тангенса.
• Расчет параметров электрических сигналов, имеющих синусоидальную форму.

Знание свойств тангенса позволяет строить математические модели реальных периодических процессов в природе и технике.