Перпендикуляр к прямой: что это такое и как построить

Перпендикуляр к прямой - одно из фундаментальных понятий геометрии, с которым мы сталкиваемся повсеместно в окружающем мире. Давайте разберемся, что это такое, каковы его свойства и как его можно построить на практике.

1. Определение перпендикуляра к прямой

Перпендикуляр к прямой - это отрезок прямой, перпендикулярной к данной, который имеет одним из своих концов точку их пересечения. Иными словами, это кратчайший путь от точки до прямой в геометрическом смысле.

Например, пешеходный переход через дорогу образует прямой угол с направлением движения машин. Это позволяет пешеходам быстрее перейти на другую сторону. Аналогично, чтобы добраться от метро до набережной реки, нужно идти перпендикулярно реке по кратчайшему пути.

Перпендикуляр в переводе с французского означает "висеть, отвес". Отсюда происходит его тесная связь с понятием высоты.

Таким образом, перпендикуляр к прямой можно представить как высоту треугольника, опущенную из некоторой точки на данную прямую. Это важное свойство перпендикуляра находит множество применений в решении геометрических задач.

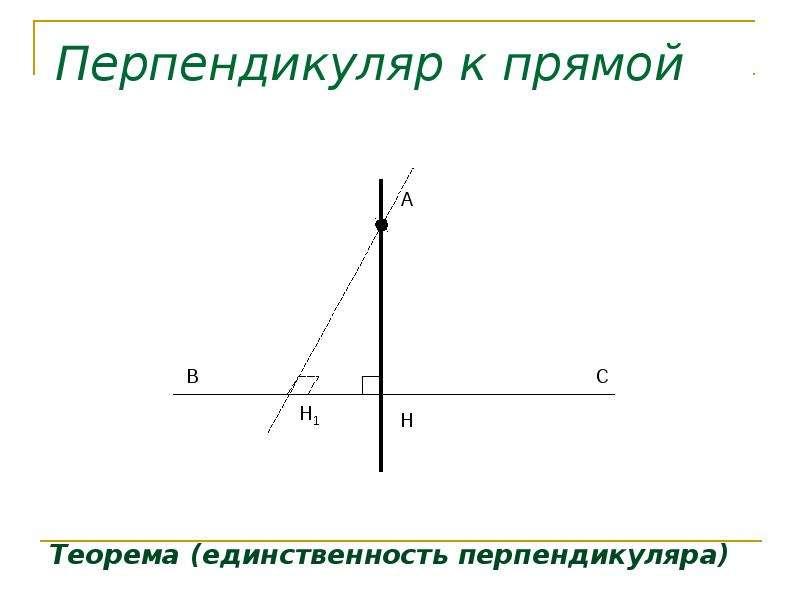
2. Уникальность перпендикуляра к прямой

Интересно, что перпендикуляр к данной прямой может быть проведен только один раз для каждой точки, не лежащей на этой прямой. Это утверждение известно как теорема о единственности перпендикуляра.

Доказательство этой теоремы основано на методе "от противного". Предположим, что через некоторую точку к данной прямой можно провести два перпендикуляра. Но тогда эти прямые должны пересечься, что невозможно по определению перпендикулярных прямых.

Простой пример, иллюстрирующий эту идею: представьте, что вы купаетесь в море недалеко от берега и увидели акулу. Вам нужно как можно быстрее доплыть до суши. Очевидно, что самый короткий путь к берегу - это перпендикуляр к береговой линии. И такой путь может быть только один.

3. Построение перпендикуляра на практике

На чертеже перпендикуляр к прямой можно построить с помощью нескольких инструментов:

1. Циркуль
2. Транспортир
3. Треугольник с прямым углом

Рассмотрим каждый способ более подробно.

Способ 1: Циркуль

Этот способ основан на свойстве окружности:

1. Из заданной точки P строим окружность, пересекающую прямую в точках A и B
2. Не меняя радиус, проводим окружности из точек A и B через точку P
3. Соединяем точку пересечения этих окружностей Q с точкой P

Полученный отрезок PQ является искомым перпендикуляром к данной прямой.

Преимущество этого способа в том, что он позволяет получить точный результат. К недостаткам можно отнести необходимость использования циркуля для построения окружностей.

Способ 2: Транспортир

Второй способ заключается в следующем:

1. Берем транспортир и откладываем 90 градусов от данной прямой
2. Соединяем полученную точку пересечения с заданной точкой

Главное преимущество - простота и скорость построения. К минусам можно отнести погрешность измерения углов.

Способ 3: Треугольник

Еще один простой способ построения перпендикуляра - использование прямоугольного треугольника:

1. Прикладываем одну сторону треугольника вдоль заданной прямой
2. Другая сторона треугольника будет являться перпендикуляром в точке пересечения

Этот метод также отличается быстротой и простотой выполнения. Основной минус - погрешность измерений из-за неточности построения самого треугольника.

4. Свойства перпендикулярных прямых

Помимо уникальности перпендикуляра, существует еще несколько важных свойств:

• Две прямые, перпендикулярные к третьей прямой, параллельны между собой
• Угол между перпендикулярными прямыми равен 90 градусов
• Прямая, перпендикулярная плоскости, перпендикулярна всем прямым этой плоскости

5. Перпендикуляр в треугольнике

Перпендикуляр тесно связан с такими элементами треугольника, как высота, медиана и биссектриса. Рассмотрим их более подробно.

Высота

Высота треугольника - это перпендикуляр, проведенный из вершины к противоположной стороне. Знание высоты позволяет вычислить площадь треугольника по формуле:

Где h - высота, a и b - стороны треугольника.

Медиана и биссектриса

В отличие от высоты, медиана и биссектриса не являются перпендикулярами к сторонам треугольника. Однако знание их свойств также важно при решении задач на вычисление площадей.

6. Применение на практике

На практике перпендикулярные прямые и плоскости находят самое широкое применение в строительстве, архитектуре, технике и даже в быту:

• Каркас здания держится на перпендикулярных элементах
• Детали машин соединяются под прямым углом
• Отвес помогает выровнять полку или картину на стене

Понимание свойств перпендикулярности в геометрии - ключ к решению многих инженерных задач!