График и особенности гиперболы: что нужно знать
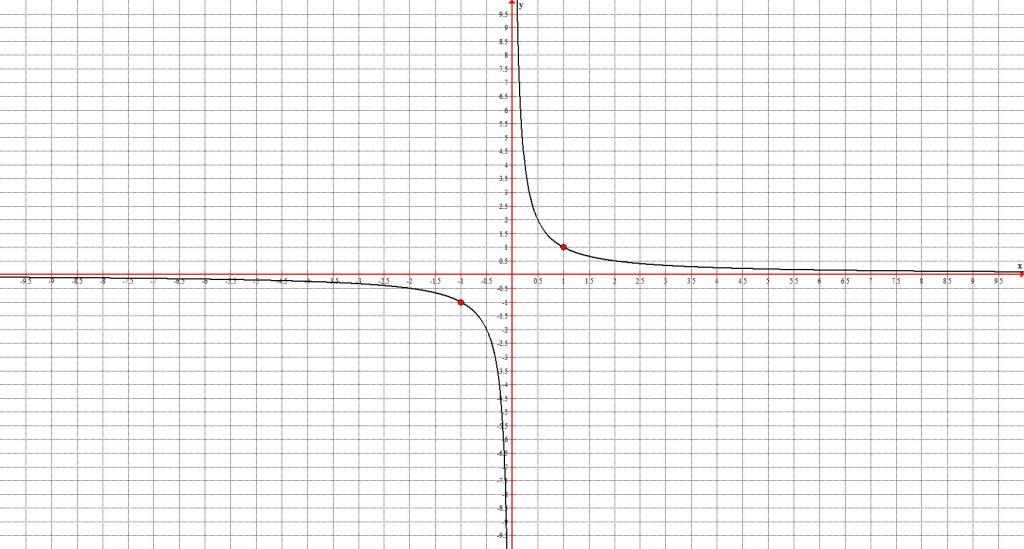
Гипербола - одна из самых загадочных кривых в математике. Ее график напоминает раскрытые крылья бабочки, устремленные в бесконечность. Давайте разберемся, что из себя представляет гипербола и как можно использовать ее удивительные свойства.
Определение гиперболы
Гипербола - это плоская кривая, которая может быть получена при пересечении кругового конуса плоскостью. От греческого "hyperbole" - чрезмерность, преувеличение. Это название гипербола получила благодаря тому, что при ее построении используется "избыточный" отрезок.
Существует несколько способов задания гиперболы:
- Уравнением второй степени:
x2/a2 - y2/b2 = 1
- Как геометрическое место точек, у которых разность расстояний до заданных фокусов постоянна
- С помощью параметрических уравнений
Гипербола состоит из двух отдельных ветвей, симметричных относительно центра. Каждая ветвь бесконечно приближается к своей асимптоте, но никогда ее не пересекает.
Элементы и свойства гиперболы
Рассмотрим основные элементы гиперболы на рисунке:
| Центр | Точка пересечения осей симметрии |
| Вершины | Точки гиперболы с наибольшим расстоянием от центра |
| Фокусы | Точки, относительно которых строится гипербола |
Гипербола обладает свойством симметрии относительно двух осей. Эти оси называются действительной и мнимой осями соответственно. Расстояния от центра гиперболы до вершин вдоль каждой из осей называются полуосями и обозначаются буквами a и b.
Построение графика гиперболы
Для построения графика гиперболы нужно:
- Определить положение центра и длины полуосей по заданному уравнению
- Найти положение вершин и асимптот
- Вычислить координаты нескольких точек гиперболы
- Построить точки и плавными линиями соединить их по порядку
Точки гиперболы удобно выбирать на равном расстоянии друг от друга вдоль всех четырех ветвей. Чем больше точек мы возьмем, тем плавнее и точнее получится график. Но для первоначального представления достаточно 4-5 точек на каждой ветви.
Рассмотрим конкретный пример построения гиперболы с полуосями a = 3, b = 2 и центром в начале координат. Сначала определяем координаты вершин (0; 2) и (0; -2), а также уравнения асимптот x = ±3. Затем вычисляем координаты точек:
| Точка 1 | (1; 1,5) |
| Точка 2 | (-1; -1,5) |
Соединяя эти точки плавной линией с учетом направления ветвей, получаем искомый график гиперболы.

Применение гиперболы
Гипербола находит широкое применение в различных областях:
Техника
В технике гиперболические конструкции используются при проектировании антенн, волноводов, оптических систем. Форма гиперболоида вращения позволяет эффективно фокусировать и отражать электромагнитные волны.

Архитектура
Арки, купола и другие архитектурные элементы, основанные на форме гиперболы, обладают хорошей прочностью при относительно небольшом расходе материала. Наиболее известные примеры - купол церкви Святого Иоанна Богослова в Москве и купол Капитолия в Вашингтоне.
Физика
С помощью гиперболы описываются различные физические процессы - движение планет, полет снарядов под углом к горизонту, распространение ударных волн и многое другое. Знание свойств гиперболы позволяет строить адекватные физические модели.
Логистика
При планировании логистических схем учитывается, что график спроса на товары зачастую имеет гиперболический характер - резкий рост с последующим насыщением. Умение прогнозировать такие тренды дает значительные преимущества.
Биология
Рост численности популяций, потребление ресурсов, распространение эпидемий - эти и другие биологические процессы математически описываются гиперболой. Анализ гиперболических моделей помогает решать важнейшие задачи в этой сфере.
Интересные факты
Гипербола присутствует не только в науке и технике, но и в искусстве. Так в архитектуре барокко гиперболические линии символизировали величие Бога, выходя за рамки человеческого разумения. А на картинах импрессионистов прием удлинения перспективы создавал ощущение бесконечно уходящего пространства.
Вычисление параметров
Часто бывает необходимо определить параметры гиперболы - полуоси, эксцентриситет, уравнение асимптот - по некоторым заданным условиям. Рассмотрим алгоритм такого вычисления.
Гипербола в задачах
Решение задач, связанных с нахождением характеристик гиперболы, значительно расширяет математический кругозор и полезно для более глубокого понимания этого удивительного вида кривых.
Похожие статьи
- Как хоронят мусульманина. Мусульманский обряд похорон
- Теория вероятности: формулы и примеры решения задач
- Практическое значение биологии в жизни человека, в медицине, в пищевой промышленности
- Известные русские химики: список, достижения, открытия и интересные факты
- Как узнать свое тотемное животное по дате рождения
- Многочлены. Разложение многочлена на множители: способы, примеры
- Чем отличается университет от института? Институт и университет: в чем разница
