"Обратно пропорционален": объяснение обратной пропорциональности, примеры, применение

Обратная пропорциональность - удивительное математическое явление, когда увеличение одной величины ведет к уменьшению другой. Этот феномен присутствует в нашей повседневной жизни чаще, чем мы думаем.

Определение обратной пропорциональности

Обратная пропорциональность - это функциональная зависимость, при которой увеличение одной величины (называемой независимой или аргументом) ведет к пропорциональному уменьшению другой величины (называемой зависимой или функцией).

Например, при постоянном расстоянии между двумя точками, чем выше скорость движения транспорта, тем меньше времени он затратит на путь. Здесь скорость и время в пути обратно пропорциональны.

Свойства обратной пропорциональности

• Если независимая величина увеличивается в n раз, то зависимая величина уменьшается в n раз
• Произведение обратно пропорциональных величин остается постоянным

Например, если скорость выросла в 2 раза, то время в пути сократится в 2 раза. Или если увеличить количество рабочих в 3 раза, то на выполнение того же объема работы потребуется в 3 раза меньше времени.

Формула обратной пропорциональности

Обратную пропорциональную зависимость между двумя величинами x и y можно выразить формулой:

y = k / x

Где k - коэффициент обратной пропорциональности. Он равен произведению любых соответствующих значений x и y.

График обратной пропорциональности

График зависимости y от x при обратной пропорциональности называется гиперболой. Он выглядит так:

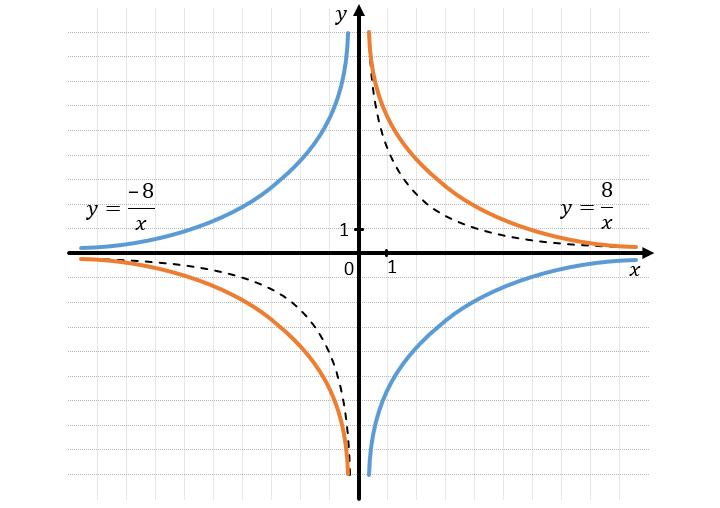
Из графика видно, что с увеличением x значение y уменьшается, и наоборот.

Примеры обратной пропорциональности в жизни

Обратная пропорциональность встречается в самых разных ситуациях:

• Скорость автомобиля и время в пути при постоянном расстоянии
• Количество рабочих и время на выполнение заданного объема работ
• Цена единицы товара и количество купленных единиц на фиксированную сумму денег

Рассмотрим последний пример подробнее. Допустим, у нас есть 500 рублей, и мы хотим купить одинаковые тетради. Чем дороже одна тетрадь, тем меньше их мы сможем купить на наши 500 рублей. Это и есть обратная пропорциональность.

Из таблицы видно, что с ростом цены количество покупаемых тетрадей падает, что подтверждает обратную пропорциональность этих величин.

Отличие от прямой пропорциональности

В отличие от обратной пропорциональности, прямая пропорциональность означает, что с увеличением одной величины другая тоже увеличивается, и наоборот.

Например, чем больше товаров положить в корзину в магазине, тем больше придется заплатить. Здесь сумма покупки прямо пропорциональна количеству товаров.

Применение обратной пропорциональности

Понимание обратной пропорциональности помогает в различных сферах деятельности:

1. Рассчитывать параметры системы по известным данным
2. Анализировать и прогнозировать ход процессов
3. Оптимизировать распределение ограниченных ресурсов

Например, зная, что на выполнение работы уходит 5 часов при 2 работниках, можно рассчитать, что при 10 работниках потребуется всего 1 час. Или, если объем данных удваивается каждый год, а пропускная способность канала связи не меняется, можно предсказать, когда возникнет перегрузка.

Таким образом, понимание обратной пропорциональности открывает новые возможности для анализа и улучшения окружающих нас систем.

Интересные факты об обратной пропорциональности

Обратная пропорциональность - довольно распространенное, но при этом удивительное явление. Рассмотрим несколько любопытных фактов о ней.

Статистика

По данным исследований, в повседневной жизни люди сталкиваются с проявлениями обратной пропорциональности гораздо чаще, чем с прямой. Однако большинство не отдают себе в этом отчета.

История открытия

Впервые обратную пропорциональность зависимость математически описал древнегреческий ученый Евклид в своих трудах по геометрии. Он отметил, что при удалении от источника света его интенсивность убывает обратно пропорционально квадрату расстояния.

Пример из психологии

Согласно исследованиям, количество близких друзей и уровень IQ человека находятся в обратной пропорциональности - чем выше интеллект, тем меньше человеку нужно друзей для ощущения счастья.

Обратная пропорциональность вне Земли

Закон всемирного тяготения гласит: сила гравитационного взаимодействия между двумя телами обратно пропорциональна квадрату расстояния между их центрами.

Значение обратной пропорциональности

Хотя обратная пропорциональность - довольно простая в математическом плане зависимость, понимание этого феномена принесло человечеству огромную пользу.

Развитие науки

Осознание явления обратной пропорциональности внесло большой вклад в развитие физики, астрономии, экономики и других наук.

Повышение эффективности

Применение принципа обратной пропорциональности позволяет оптимизировать многие процессы в промышленности, бизнесе, на транспорте и в других сферах.

Технологический прогресс

Понимание закономерностей обратной пропорциональности послужило толчком к разработке новых технологий в области энергетики, связи, вычислительной техники.

Таким образом, это удивительное математическое явление оказало глубокое влияние на развитие нашей цивилизации.