Множество Мандельброта: определение, структуры, применение

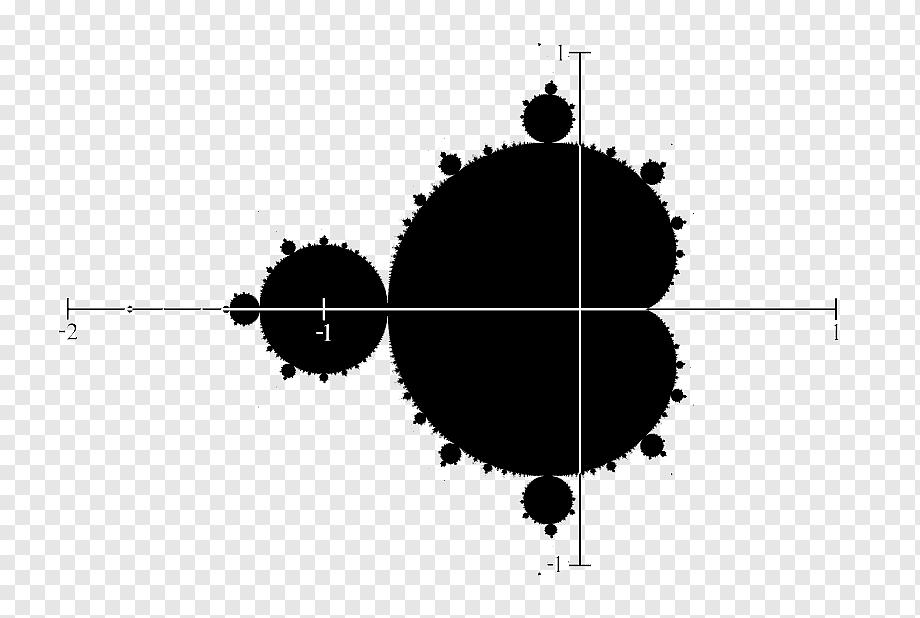
Множество Мандельброта - один из самых знаменитых математических объектов, скрывающий в своих недрах целые вселенные удивительной красоты. Давайте попробуем приоткрыть завесу тайны и заглянуть в бездонные глубины этого фрактального чуда.

История открытия

Впервые идея исследования множества появилась в 19 веке у французского математика Пьера Фату. Он изучал динамику простого итеративного процесса zn+1 = zn2 + c, то есть последовательного возведения комплексного числа в квадрат и прибавления константы. Этот процесс может либо сходиться к конечному пределу, либо уходить на бесконечность. Фату вручную проводил вычисления для разных значений параметра c и обнаружил интересные закономерности в поведении орбит точек.

Однако по-настоящему революционный прорыв произошел лишь в 20 веке с приходом компьютеров и новых методов визуализации. В 1975 году франко-американский математик Бенуа Мандельброт в книге «Фрактальная геометрия природы» впервые использовал термин «фрактал» для описания таких самоподобных геометрических объектов и ввел понятие множества Мандельброта.

Множество Мандельброта определяется как совокупность всех значений параметра c комплексной плоскости, для которых итеративная последовательность формулы Фату остается ограниченной, то есть не уходит на бесконечность.

В 1970-80-х годах появились первые компьютерные изображения множества Мандельброта, полученные с помощью алгоритма «метода бегства». Эти первые в истории фрактальные картины поразили ученых невообразимой сложностью структуры и скрытой в ней красотой.

Математическое определение

Множество Мандельброта определяется довольно простым рекуррентным соотношением, но скрывает в себе поистине неисчерпаемое богатство форм, структур и закономерностей.

Формально, пусть дана функция fc(z) = z2 + c, где z - комплексное число, а c - некоторый комплексный параметр. Рассмотрим последовательность чисел, заданную рекуррентно:

1. z₀ = 0
2. z_n+1 = (z_n)² + c, где n = 0, 1, 2...

Тогда множество Мандельброта M определяется как совокупность всех значений параметра c, для которых последовательность {z_n} остается ограниченной, то есть:

M = {c Є C : существует R > 0 : |z_n| < R для всех n}

Свойства множества Мандельброта

Несмотря на простоту определения, множество Мандельброта обладает удивительными и зачастую неочевидными свойствами.

Связность

В 1980 году математики Дауди и Хаббард доказали, что множество Мандельброта является связным. Это означает, что любую точку внутри множества можно соединить с любой другой непрерывной кривой, не выходящей за его пределы. На первый взгляд это кажется удивительным, ведь визуально множество имеет множество разрывов и "мостов".

Самоподобие

Еще одно поразительное свойство множества Мандельброта - его самоподобие . Это значит, что при любом увеличении множества в окрестности любой его точки будут обнаруживаться все новые детали, повторяющие общий рисунок всей структуры. Элементы самоподобия проявляются на всех масштабах - от мельчайших деталей до крупных фрагментов.

Алгоритмы построения

Для построения графических изображений множества Мандельброта используются различные алгоритмы. Рассмотрим некоторые из них.

Внутренняя структура

При детальном рассмотрении внутри множества Мандельброта обнаруживается сложная иерархическая структура из самоподобных элементов.

Нерешенные загадки

Несмотря на многолетнее изучение, множество Мандельброта до сих пор хранит немало тайн и загадок, ждущих своих исследователей.

Описание алгоритма

Алгоритм метода бегства состоит в следующем:

1. Выбирается некоторая область на комплексной плоскости параметра c, которую нужно исследовать
2. Эта область разбивается на пиксели заданного разрешения
3. Для каждого пикселя (значения параметра c):
   Вычисляется последовательность {z
   _n
   } с начальным условием z
   ₀
   = 0 Если модуль |z
   _n
   | превысил некоторое пороговое значение R (например, 2), считается, что последовательность "убежала" на бесконечность, и точка не принадлежит множеству Если за максимальное число итераций модуль |z
   _n
   | не превысил R, считается, что точка принадлежит множеству
4. Принадлежность точки множеству кодируется цветом соответствующего пикселя

Оптимизации алгоритма

Существует несколько методов оптимизации этого алгоритма.

Использование кардиоиды

Одна из оптимизаций основана на том, что все точки внутри кардиоиды гарантированно принадлежат множеству. Поэтому для них нет необходимости проводить итеративные вычисления - их сразу можно закрашивать.

Детализация внутренней структуры

При больших увеличениях внутри множества Мандельброта становятся различимы все более мелкие детали его структуры:

• Видна центральная кардиоида и окружающие ее концентрические окружности
• Внутри каждой окружности просматриваются еще более мелкие копии тех же структур
• Этот процесс повторяется до бесконечности на всех масштабах

Так проявляются различные уровни самоподобия множества Мандельброта.

Применение в компьютерной графике

В компьютерной графике множество Мандельброта используется как источник уникальных фрактальных текстур и узоров. Например, его можно применять для:

• Генерации фона
• Создания орнаментов
• Моделирования природных ландшафтов
• Спецэффектов

Влияние на искусство

Завораживающие узоры множества Мандельброта часто используются художниками и дизайнерами как источник вдохновения. Его мотивы можно увидеть в таких направлениях, как:

• Цифровая живопись
• Абстрактная скульптура
• Архитектура
• Мода и текстиль

Нерешенные загадки

Некоторые открытые вопросы о множестве Мандельброта, ждущие своих исследователей:

• Гипотеза о локальной связности
• Измерение размерностей границы
• Влияние параметра c на хаотичность динамики

Разгадка этих и других загадок поможет еще глубже проникнуть в удивительный мир множества Мандельброта.