Как составить пропорцию: руководство

Пропорции присутствуют в нашей жизни повсюду: в архитектуре, живописи, кулинарии и даже в обычных бытовых задачах. Умение составлять верные пропорции очень полезно и порой просто необходимо.
Что такое пропорция и зачем она нужна
Итак, давайте разберемся, что же такое пропорция.
Пропорцией называют равенство двух отношений.
Например, отношение 3 к 5 равно отношению 6 к 10. Это и есть пропорция:
3/5 = 6/10
Пропорции используются в самых разных областях:
- В строительстве - для расчета пропорций зданий и сооружений;
- В изобразительном искусстве - для передачи правильных пропорций объектов;
- В музыке - для настройки музыкальных инструментов;
- В кулинарии - для расчета пропорций ингредиентов в рецептах.
Как видите, пропорции помогают устанавливать гармоничные соотношения между частями целого. Поэтому умение их составлять очень полезно.
Как записать и прочитать пропорцию
Как составить пропорцию из двух отношений? Все просто - нужно приравнять эти отношения.
Например, имеются отношения 5 к 20 и 3 к 12. Чтобы из них получить пропорцию, приравниваем:
5/20 = 3/12
То есть отношение 5 к 20 равно отношению 3 к 12.
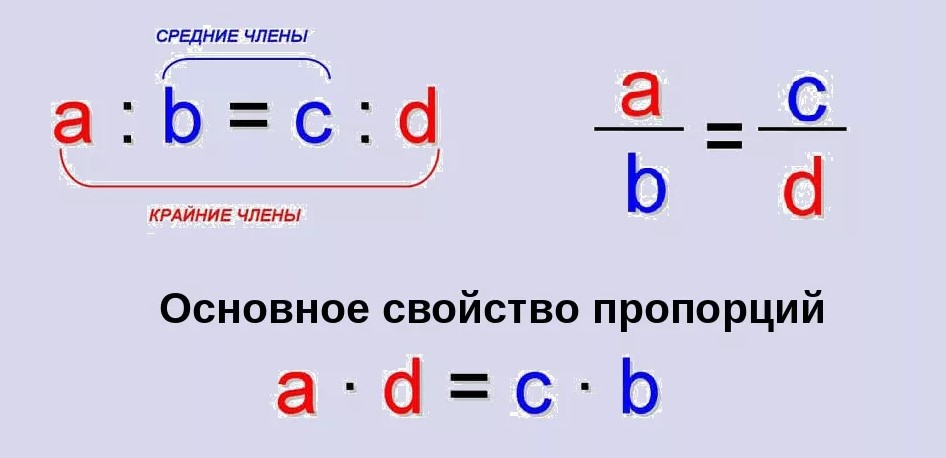
С помощью букв пропорцию можно записать вот так:
a/b = c/d
Прочитать такую пропорцию нужно так: "а относится к b, как с относится к d".
Например, пропорцию x/3 = 5/15 читают: "икс относится к трем, как пять относится к пятнадцати".
Помимо дробной записи, пропорцию можно изобразить и в виде обычной дроби:
5:20 = 3:12
Выбирайте удобный для вас формат записи пропорций.
| Дробная запись | 5/20 = 3/12 |
| Запись с помощью букв | a/b = c/d |
| Запись с помощью двоеточия | 5:20 = 3:12 |
Теперь разберемся, как составить верную пропорцию.
Как составить верную пропорцию
Чтобы составить пропорцию правильно, нужно следовать ее основному свойству:
Произведение крайних членов пропорции равно произведению ее средних членов.
Это свойство позволяет проверить, верна ли заданная пропорция. Давайте разберем на примере:
Проверим, верна ли пропорция 6:3 = 10:5.
- Находим произведение крайних членов: 6 * 5 = 30.
- Находим произведение средних членов: 3 * 10 = 30.
- Произведения крайних и средних членов равны. Значит, пропорция верна.
Точно так же можно проверять любые пропорции, составленные вами.
Как составить пропорцию шаг за шагом
Итак, давайте разберем пошаговый алгоритм составления пропорции:
- Запишите два отношения, которые вы хотите приравнять.
- Приравняйте эти отношения с помощью знака равенства.
- Проверьте полученную пропорцию, перемножив крайние и средние члены.
Потренируйтесь в составлении собственных пропорций, следуя этому алгоритму. Уверены, все получится!
Как найти неизвестный член с помощью основного свойства
Часто в пропорциях бывает один неизвестный член. Его можно найти, опираясь на основное свойство пропорций.
Например, в пропорции a/3 = 5/15 неизвестна величина a. Чтобы ее определить, составим уравнение:
a/3 = 5/15
a * 15 = 5 * 3
a = 5
Как видите, неизвестный член пропорции нашелся легко, поскольку мы знаем основное свойство пропорций.
Примеры решения уравнений с пропорциями
Рассмотрим еще несколько примеров нахождения неизвестного в пропорциях.
Найдем x в пропорции 0,25:x = 3,75:3:
0,25 * 3 = x * 3,75
0,75 = 3,75x
x = 0,2
Определим k в пропорции 1/4 : k = 3/6:
1/4 * 6 = k * 3
3/2 = k
k = 0,5
Рекомендации по нахождению неизвестного
Чтобы без труда находить неизвестный член пропорции:
- Записывайте основное свойство пропорции в виде уравнения;
- Перемножайте крайние и средние члены;
- Выражайте неизвестную величину.

Задачи на применение пропорций
Рассмотрим несколько практических задач, где потребуются навыки работы с пропорциями.
-
За 8 часов бригада рабочих выкопала 16 метров траншеи. Сколько метров траншеи выкопает такая же бригада за 5 часов?
Решение: Составляем и решаем пропорцию с неизвестным х:
8 ч : 16 м = 5 ч : х мх = 10 (м) -
Смесь для выпечки состоит из муки, сахара и масла в соотношении 5:2:1. Сколько грамм масла нужно добавить к 500 г муки?
Решение: В пропорции ищем неизвестный вес масла х:
500 г : 5 = х г : 1x = 100 (г)
Потратьте время на решение таких заданий - и работа с пропорциями перестанет быть для вас сложной!
Похожие статьи
- Известные русские химики: список, достижения, открытия и интересные факты
- Какие бывают предложения по цели высказывания и по интонации? Виды предложений по цели высказывания
- Где провести выпускной для 4 класса: интересные идеи и рекомендации
- Женские интимные прически: фото, виды и технология выполнения
- Птица ударилась в окно: что означает примета? Птица ударилась в окно - к чему это?
- Где живет слепая ясновидящая баба Нина: адрес и отзывы
- Характеристика Льва-женщины. Знак Зодиака Лев: описание
