Что такое треугольник? Определение, виды и свойства

Треугольник - одна из самых простых, но в то же время удивительных геометрических фигур. Уже в глубокой древности люди начали изучать его свойства, а сегодня без знаний о треугольнике не обходится ни одна отрасль науки. Давайте разберемся, что же такое треугольник и почему он так важен.

Определение треугольника

Итак, что такое треугольник? Треугольник - это геометрическая фигура, образованная тремя точками, которые не лежат на одной прямой, и тремя отрезками, соединяющими эти точки. Иными словами, для построения треугольника нужно взять три точки и соединить их так, чтобы получилось три отрезка.

Основными элементами треугольника являются:

• Вершины - точки, из которых строится треугольник (обозначаются буквами)
• Стороны - отрезки, соединяющие вершины (обозначаются строчными буквами)
• Углы - углы при вершинах треугольника (обозначаются греческими буквами)

На рисунке изображен пример треугольника со всеми основными элементами:

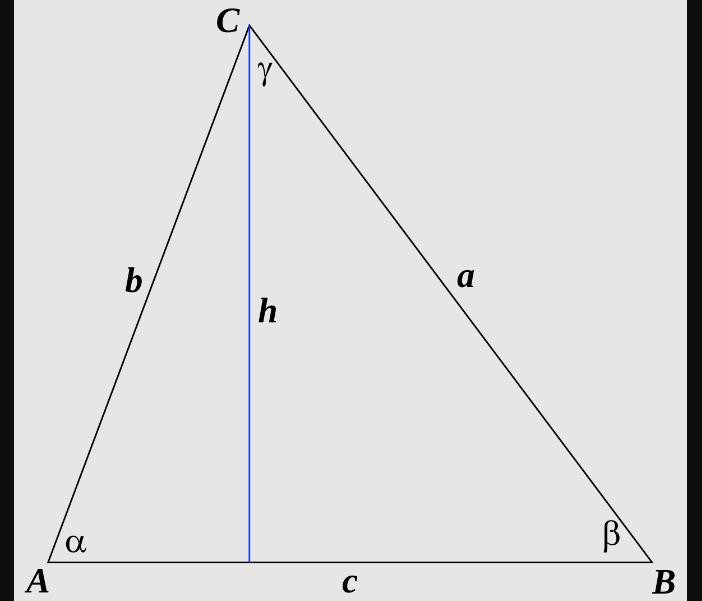
Здесь точки A, B и C - это вершины, отрезки AB, BC и CA - стороны, а углы при вершинах обозначены греческими буквами α, β и γ.

Виды треугольников

Существует несколько способов классификации треугольников в зависимости от их свойств. Рассмотрим основные из них.

По соотношению углов

По углам различают:

1. Остроугольный треугольник - все углы острые (меньше 90°)
2. Прямоугольный треугольник - один угол равен 90°
3. Тупоугольный треугольник - один угол тупой (больше 90°)

По соотношению сторон

По сторонам бывают:

• Разносторонний треугольник - все стороны разной длины
• Равнобедренный треугольник - две стороны равны
• Равносторонний треугольник - все стороны равны

Помимо основных элементов, у треугольника есть и другие важные характеристики.

Периметр треугольника

Периметр треугольника - это сумма длин всех его сторон:

P = a + b + c

где a, b и c - длины сторон треугольника.

Замечательные линии треугольника

К замечательным линиям треугольника относят:

• Высоту - перпендикуляр из вершины к противоположной стороне
• Медиану - отрезок из вершины к середине противоположной стороны
• Биссектрису - луч, делящий угол треугольника пополам

Эти линии играют важную роль при изучении свойств треугольника.

Таким образом, теперь вы знаете, что такое треугольник, его основные элементы и виды. В следующих частях статьи мы подробнее рассмотрим свойства этой удивительной геометрической фигуры.

Основные свойства треугольника

Рассмотрим некоторые важные свойства, которыми обладает любой треугольник.

Сумма углов треугольника

Одним из фундаментальных свойств является то, что сумма всех трех углов треугольника всегда равна 180°. Это значит, что если известны два угла треугольника, то третий угол можно найти по формуле:

γ = 180° - α - β

где α и β - известные углы, а γ - искомый угол.

Внешние углы треугольника

Еще одним важным понятием являются внешние углы треугольника. Это углы, образованные продолжением двух сторон треугольника.

Внешний угол равен сумме двух внутренних углов, не смежных с ним. Например, на рисунке внешний угол α равен сумме углов γ и β.

Неравенство треугольника

Существует неравенство, связывающее длины сторон треугольника:

a + b > c

Оно означает, что сумма любых двух сторон треугольника больше третьей стороны. Это важное свойство часто используется при решении задач с треугольниками.

Признаки равенства треугольников

Для того чтобы установить, равны ли два треугольника, не обязательно их накладывать друг на друга. Существуют три основных признака равенства:

1. По двум сторонам и углу между ними
2. По стороне и двум прилежащим углам
3. По трем сторонам

Эти признаки позволяют определять равенство треугольников гораздо проще.

Применение треугольников

Знания о свойствах треугольников широко применяются на практике - в строительстве, архитектуре, машиностроении и многих других областях.

Использование в строительстве

В строительстве треугольники широко используются при возведении каркасов зданий и сооружений. Благодаря своей устойчивой геометрической форме, треугольные конструкции обладают высокой несущей способностью и позволяют равномерно распределять нагрузку.

Например, при проектировании крыш часто применяют треугольные фермы - легкие и прочные конструкции из стержней. Их использование позволяет перекрывать большие пролеты без дополнительных опор.

Применение в топографии

В топографии и геодезии треугольники используются при проведении съемок местности и определении координат точек. На местности размечают треугольную сеть из пунктов с известными координатами, а затем выполняют привязку остальных точек к этой сети.

Благодаря тому, что длины сторон и углы треугольника однозначно определяют его форму и положение, триангуляционные методы обеспечивают высокую точность измерений.

Применение в промышленности

В машиностроении треугольники широко используются при конструировании и расчетах деталей машин. Например, зубчатые колеса часто делают треугольной формы, что обеспечивает плавную и бесшумную работу.

Кроме того, благодаря жесткости треугольника, его часто используют в конструкциях, которые должны выдерживать большие нагрузки - рамах, фермах и т.д.

Треугольник в искусстве и архитектуре

Несмотря на кажущуюся простоту, треугольная форма широко используется и в творчестве - живописи, скульптуре, архитектуре. Острые и тупые углы, разный наклон сторон позволяют создавать интересные композиции, игру светотени.

Треугольные фронтоны, арки, пилоны придают зданиям выразительность, завершенность. А использование равносторонних треугольников создает ощущение гармонии и соразмерности.

Использование треугольников в дизайне

В дизайне интерьеров и ландшафта треугольные формы также находят широкое применение благодаря своим эстетическим качествам.

Треугольные ниши, полки, декоративные элементы позволяют визуально расширить пространство, сделать комнату более выразительной. А использование равносторонних треугольников в отделке стен и пола создаст ощущение гармонии.

Треугольники в логотипах

Многие известные бренды и компании используют в своих логотипах треугольники, подчеркивая таким образом динамику развития, технологичность или стабильность своего бизнеса.

Например, знаменитый логотип «Play» компании Google выполнен в виде равностороннего треугольника, символизируя открытость, честность и прозрачность бизнеса.

Математические вычисления с треугольниками

В математике треугольники используются при решении множества задач - вычислении площадей, углов, определении расстояний и координат точек.

Зная стороны и углы треугольника, можно вычислить его площадь, воспользовавшись формулами, выведенными еще в античные времена. Эти классические формулы до сих пор активно используются для математических расчетов в самых разных областях.

Применение треугольников в оптике

Благодаря своим геометрическим свойствам, треугольники нашли применение и в оптических системах - телескопах, микроскопах, фотоаппаратах.

Например, в конструкции зеркальных телескопов используются треугольные зеркала, которые обеспечивают нужную траекторию прохождения световых лучей и фокусировку изображения.

Треугольники в программировании и компьютерной графике

При создании трехмерных моделей и визуализаций в компьютерных программах треугольники являются одним из базовых графических примитивов.

Из треугольников формируются полигональные сетки, которые затем обрабатываются для создания реалистичных 3D-моделей персонажей, транспорта, архитектурных сооружений и других объектов.

Применение знаний о треугольниках в повседневной жизни

Даже в быту знания о свойствах треугольников могут быть весьма полезны - например, при самостоятельном ремонте или строительстве мебели, садовых построек.

Умение рассчитать углы, длины сторон, необходимое количество материалов для треугольной крыши или основания - все это поможет сделать работу качественно и рационально использовать ресурсы.