Как возвести в отрицательную степень число: алгоритм и примеры

Возведение числа в отрицательную степень на первый взгляд кажется загадочным. На самом деле, это довольно простая операция, широко используемая в математике и естественных науках.

Теоретические основы

Чтобы разобраться с отрицательными степенями, давайте начнем с определений.

Отрицательная степень числа – это число, возведенное в степень с отрицательным показателем.

Например, запись 5^-2 означает, что число 5 возведено в степень -2. При этом важно помнить два фундаментальных свойства степени:

1. Любое число, возведенное в нулевую степень, равно 1.
2. Число, возведенное в степень 1, равно самому себе.

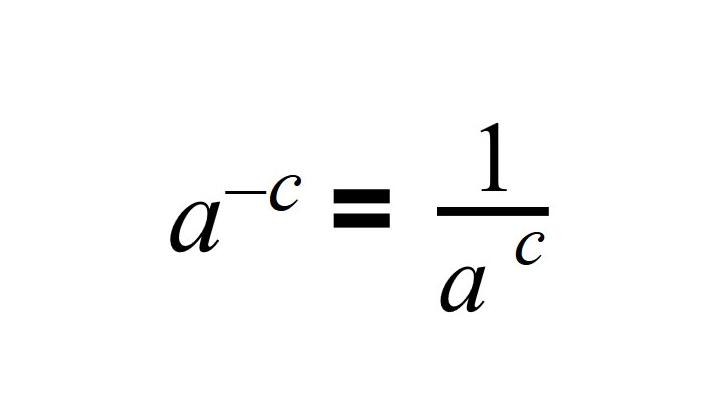
Правило возведения в отрицательную степень

Исходя из этих свойств, можно сформулировать правило для отрицательных степеней:

Число, возведенное в отрицательную степень n, равно единице, разделенной на это число, возведенное в степень |n|.

Где |n| – модуль числа n, то есть его абсолютное значение. Давайте разберем это правило на примерах:

• 5^-3 = 1 / (5³) = 1 / 125 = 0,008
• 2^-2 = 1 / (2²) = 1 / 4 = 0,25

Алгоритм вычисления

Чтобы вычислить любую отрицательную степень, можно использовать следующий алгоритм:

1. Записать число и отрицательный показатель степени
2. Показатель по модулю записать как положительный
3. Возвести число в полученную положительную степень
4. Разделить 1 на полученный результат

Давайте опробуем этот алгоритм для числа 7^-4:

1. Задано: 7^-4
2. |(-4)| = 4
3. 7⁴ = 2401
4. 1 / 2401 = 0,000416

Ответ: 7<-4> = 0,000416

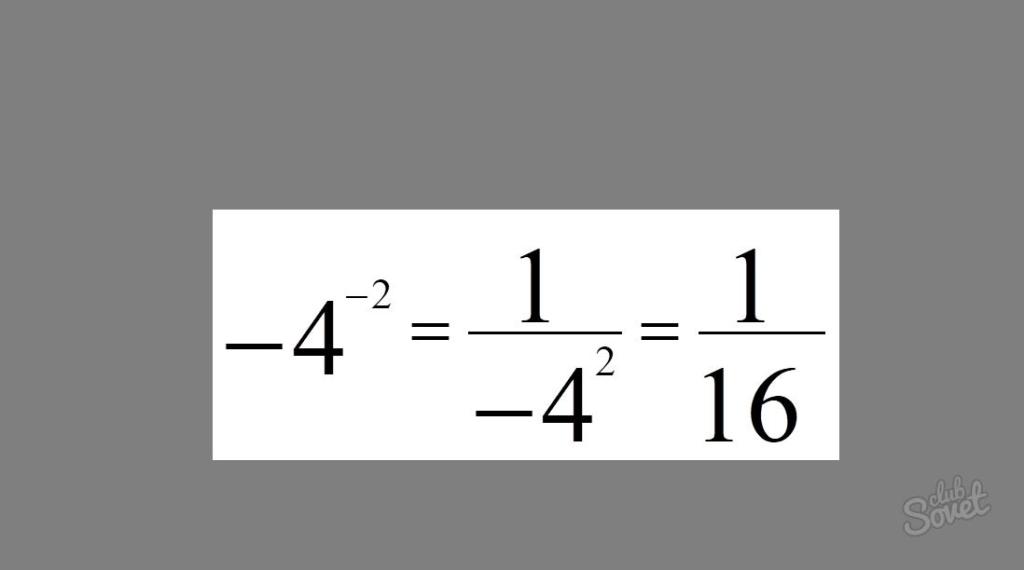
Практическое применение

Хотя отрицательные степени могут показаться абстрактным математическим понятием, у них есть множество практических применений.

В математических вычислениях

Отрицательные степени позволяют компактно записывать дробные величины. Например:

• 0,2 = 2^-1
• 0,125 = 1 / 8 = 2^-3

В физических формулах

Многие физические законы содержат отрицательные степени. Они описывают обратную зависимость величин.

Например, закон всемирного тяготения:

F ~ 1 / r²

Где F – сила, r – расстояние. Чтобы найти силу, нужно расстояние возвести в степень -2.

В экономике и финансах

Отрицательные степени используются в экономических формулах. Например, для расчета эластичности спроса по цене:

Эс = %ΔQ / %ΔP

Здесь %ΔQ – изменение объема спроса в процентах, %ΔP – изменение цены в процентах. Чтобы найти эластичность, цену возводят в степень -1.

При моделировании процессов

Отрицательные степени часто возникают в математических моделях реальных процессов. Например, при описании затухающих колебаний, распространении волн, теплопередаче.

Вот пример затухающей гармонической функции:

y = Acos(ωt + φ)e^-λt

Здесь показатель затухания λ – всегда отрицательное число.

Примеры практических задач и расчетов

Давайте теперь более подробно разберем конкретные примеры использования отрицательных степеней.

Задача 1. Расчет сопротивления резистора (физика)

Известно, что электрическое сопротивление резистора определяется по формуле:

R = ρ·l/S

Здесь ρ - удельное сопротивление материала резистора, l - его длина, S - площадь поперечного сечения.

Требуется найти сопротивление резистора с параметрами:

• ρ = 2·10^-6 Ом·м
• l = 30 см = 0,3 м
• S = 0,5 мм² = 0,5·10^-6 м²

Решение:

Подставляем значения в формулу:

R = (2·10^-6 Ом·м) · (0,3 м) / (0,5·10^-6 м²)

R = 1,2·10⁶ / 0,5·10^-6 = 1200 Ом

Ответ: сопротивление резистора равно 1200 Ом.

Задача 2. Расчет эластичности спроса по цене

Один предприниматель продает сувениры. За прошлый год при цене в 10 долларов он продал 500 изделий. После того, как он поднял цену до 15 долларов, продажи упали до 300 штук.

Требуется: найти эластичность спроса по цене для его сувениров.

Решение:

Сначала находим изменение объема спроса в %:

%ΔQ = (300 - 500) / 500 · 100% = -40%

Затем изменение цены в %:

%ΔP = (15 - 10) / 10 · 100% = 50%

Подставляем значения в формулу эластичности спроса по цене:

Эс = -40% / 50% = -0,8

Ответ: эластичность спроса по цене равна -0,8.