Таблицы значений синуса и косинуса в тригонометрии
Тригонометрия является фундаментальной математической дисциплиной с обширными практическими применениями в науке и технике. В данной статье речь пойдет о таком важном инструменте тригонометрии, как таблицы значений основных тригонометрических функций - синуса и косинуса.
История возникновения тригонометрических таблиц
Первые тригонометрические таблицы появились еще в глубокой древности. Так, в Древнем Египте и Вавилоне уже использовались приближенные значения синусов и косинусов для решения задач, связанных со строительством храмов, дворцов и других сооружений. Однако тригонометрия как самостоятельная дисциплина начала складываться только в античной Греции в рамках изучения свойств геометрических фигур.
Пифагорейцы впервые установили взаимосвязь между отношениями сторон прямоугольного треугольника и углами, что и положило начало тригонометрии.
Великий вклад в развитие тригонометрии внесли также ученые Индии и арабского Востока в период средневековья. Они предложили использовать в качестве основной меры угла не градус, а радиан. Кроме того, именно индийские и арабские математики впервые составили достаточно подробные таблицы значений тригонометрических функций, в том числе синуса и косинуса.
Европейские тригонометрические таблицы 16-18 веков
В Европе первые обширные таблицы синусов и косинусов были рассчитаны и опубликованы в 16 веке немецким математиком Ретиком. Позже, в 17 веке, появились еще более подробные и точные таблицы, составленные Винсентом и Брадисом. Эти таблицы активно использовали инженеры, физики, мореплаватели для своих вычислений вплоть до появления компьютеров.
Современные тригонометрические таблицы
В наши дни наиболее широко применяются два основных типа таблиц значений тригонометрических функций:
- Таблица основных значений
- Таблицы Брадиса: таблица синусов и косинусов таблица тангенсов и котангенсов
Рассмотрим их подробнее.

Таблица основных значений
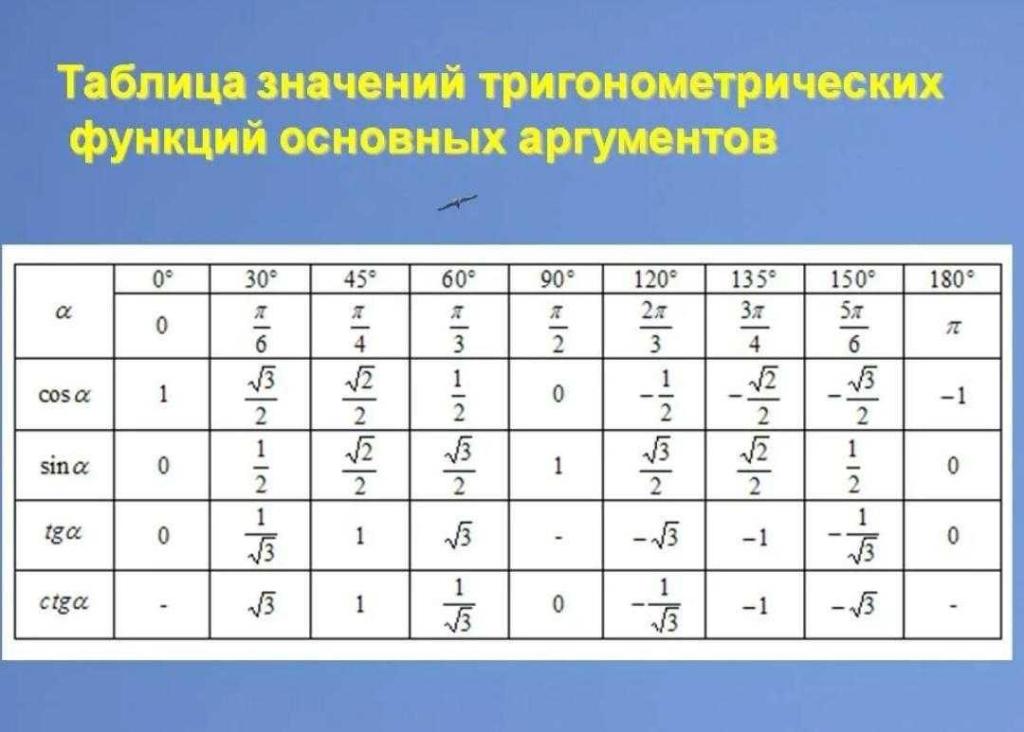
Эта таблица содержит значения синуса, косинуса и других тригонометрических функций для основных углов 0°, 30°, 45°, 60° и 90° (0, π/6, π/4, π/3, π/2 радиан). Иногда в таблицу также включают значения для дополнительных углов вплоть до 360° (2π радиан). Таблицу основных значений удобно использовать для быстрой оценки величины тригонометрических функций.
| Угол α | 0° | 30° | 45° | 60° | 90° |
| sin α | 0 | 1/2 | √2/2 | √3/2 | 1 |
| cos α | 1 | √3/2 | √2/2 | 1/2 | 0 |
Таблицы Брадиса
Эти таблицы содержат значения синусов, косинусов, тангенсов и котангенсов с точностью до четырех знаков после запятой для всех углов от 0 до 90 градусов с шагом в одну угловую минуту. Таблицы Брадиса до сих пор широко используются в инженерных расчетах, навигации и других областях, требующих высокой точности вычислений.
Для удобства таблицы Брадиса разделены на две части:
- Таблица синусов и косинусов
- Таблица тангенсов и котангенсов
Рассмотрим их более подробно.

Таблица синусов и косинусов
Эта таблица позволяет для заданного угла найти значения синуса и косинуса с высокой точностью. Для этого в таблице указывается количество градусов и минут искомого угла. Затем по специальным поправочным столбцам уточняется значение в зависимости от количества секунд.
Например, из таблицы Брадиса можно найти, что sin(20°15′) = 0,3420.
Таблица тангенсов и котангенсов
Аналогичным образом устроена таблица для нахождения значений тангенсов и котангенсов углов с точностью до одной угловой минуты. С ее помощью, к примеру, можно определить, что tg(45°20′) = 1,0296.
Таким образом, таблицы Брадиса до сих пор являются незаменимым инструментом для инженеров, физиков, геодезистов и других специалистов, нуждающихся в высокоточных вычислениях значений тригонометрических функций.
Как пользоваться тригонометрическими таблицами
Для эффективного использования тригонометрических таблиц необходимо четко представлять принцип их работы и уметь правильно находить в них нужные значения. Рассмотрим основные приемы работы с таблицами на конкретных примерах.
Поиск значений в таблице основных значений
Таблица основных значений позволяет очень быстро находить приближенные значения тригонометрических функций для стандартных углов. Для этого достаточно в соответствующей строке найти нужное значение угла. Например, значение cos 60° = 0.5.
Использование таблиц Брадиса
При работе с таблицами Брадиса нужно:
- Определить количество градусов и минут искомого угла
- Найти это значение в соответствующей таблице
- При необходимости внести поправку на количество секунд с помощью дополнительных столбцов
Рассмотрим конкретный пример. Требуется найти sin 37°24′18′′. Сначала в таблице синусов находим значение для 37°24′: 0.5882. Затем складываем поправку на 18 секунд: 0.0006. Итого: sin 37°24′18′′ = 0.5888.

Примеры решения задач с помощью таблиц
Рассмотрим классическую задачу на использование таблиц Брадиса:
В треугольнике ABC угол A равен 15°20′30′′. Найти cos A, если известно, что c = 5 см, а b = 4 см.
Решение:
- По таблице Брадиса находим значение cos 15°20′: 0.9659.
- С учетом поправки на 30 секунд получаем: cos 15°20′30′′ = 0.9656.
- Используя определение косинуса и теорему Пифагора:
- c
- = a
- + b
- c = √(a
- +b
- ) = √(4
- +5
- ) = √41 см cos A = b/c = 4/√41
- 0.9656 = 4/√41
- Откуда находим искомый ответ: √41 = 7 см.
Ошибки при работе с таблицами
Часто встречающиеся ошибки:
- Поиск значений тригонометрических функций для углов больше 90° (например, 120°)
- Нахождение в таблицах котангенсов вместо тангенсов и наоборот
- Неверный учет знака при применении поправок из дополнительных столбцов
- Неправильное определение количества градусов, минут и секунд заданного угла
Для избежания таких ошибок следует четко представлять идеологию работы тригонометрических таблиц и регулярно решать задачи на их применение.
Похожие статьи
- К чему снятся змеи женщине? Толкование снов
- Что изучает история? Зачем нужно изучать историю? История мира
- Птица ударилась в окно: что означает примета? Птица ударилась в окно - к чему это?
- Гуманитарные профессии. Профессии социально-гуманитарного профиля
- Белоруссия или Беларусь: как правильно говорить и писать?
- Особенности российской модернизации начала 20 века. История России
- Устное народное творчество: виды, жанры произведений и примеры
