Угол между касательной и хордой: теоремы и вычисления

Угол между касательной и хордой - один из ключевых элементов геометрии, позволяющий решать многие задачи. Чтобы грамотно оперировать этим понятием на практике, нужно разобраться в соответствующих теоремах и формулах. Давайте вместе изучим основы вычисления угла между касательной и хордой окружности.

Основные определения и обозначения

Начнем с базовых понятий.

• Окружность - замкнутая кривая, все точки которой равноудалены от центра.
• Хорда - отрезок, соединяющий две точки окружности.
• Касательная - прямая, имеющая с окружностью ровно одну общую точку.

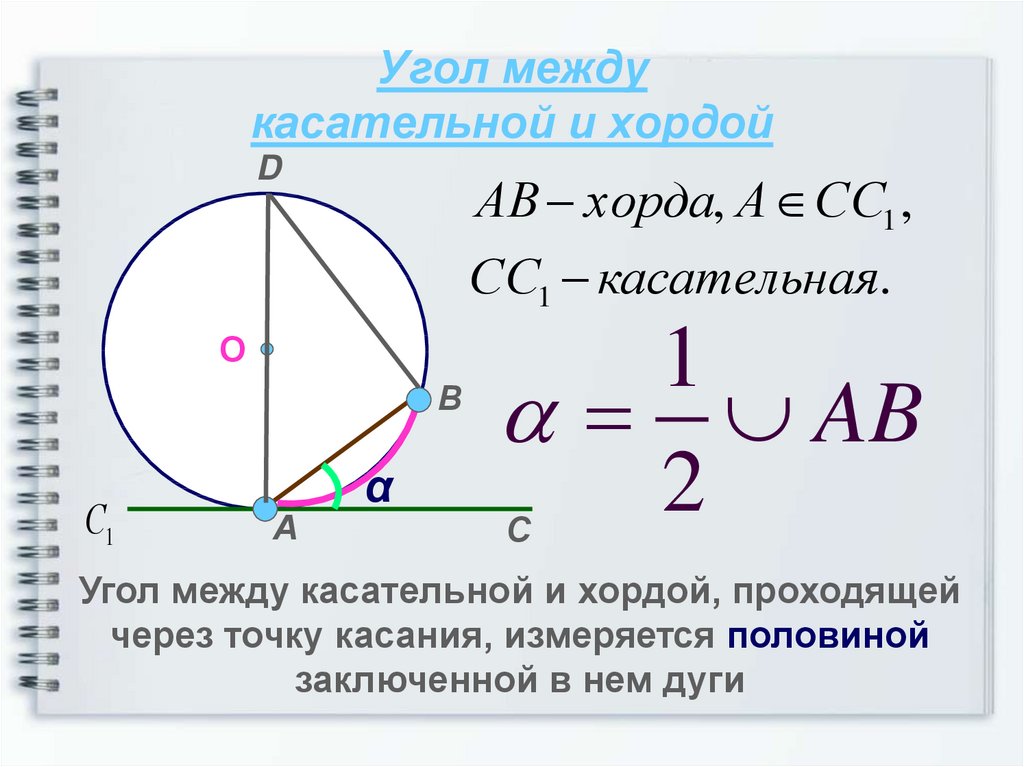
На рисунке используются следующие обозначения элементов:

• O - центр окружности
• AB - хорда окружности
• BC - касательная к окружности
• α - искомый угол между касательной и хордой

При измерении углов приняты следующие правила знаков:

1. углы, меньшие 180°, считаются положительными;
2. углы, большие 180°, считаются отрицательными.

Связь угла с центральным углом

Помимо дуги и вписанного угла, рассматриваемый нами угол между касательной хордой связан и с центральным углом:

• Центральный угол AOB опирается на ту же дугу AB, что и угол ABC;
• Градусная мера центрального угла равна величине дуги AB;
• Градусная мера угла ABC составляет половину от дуги AB.

Отсюда получаем:

∠ABC = 0,5 * ∠AOB

Вычисление угла между касательной хордой проведенной" в точке касания

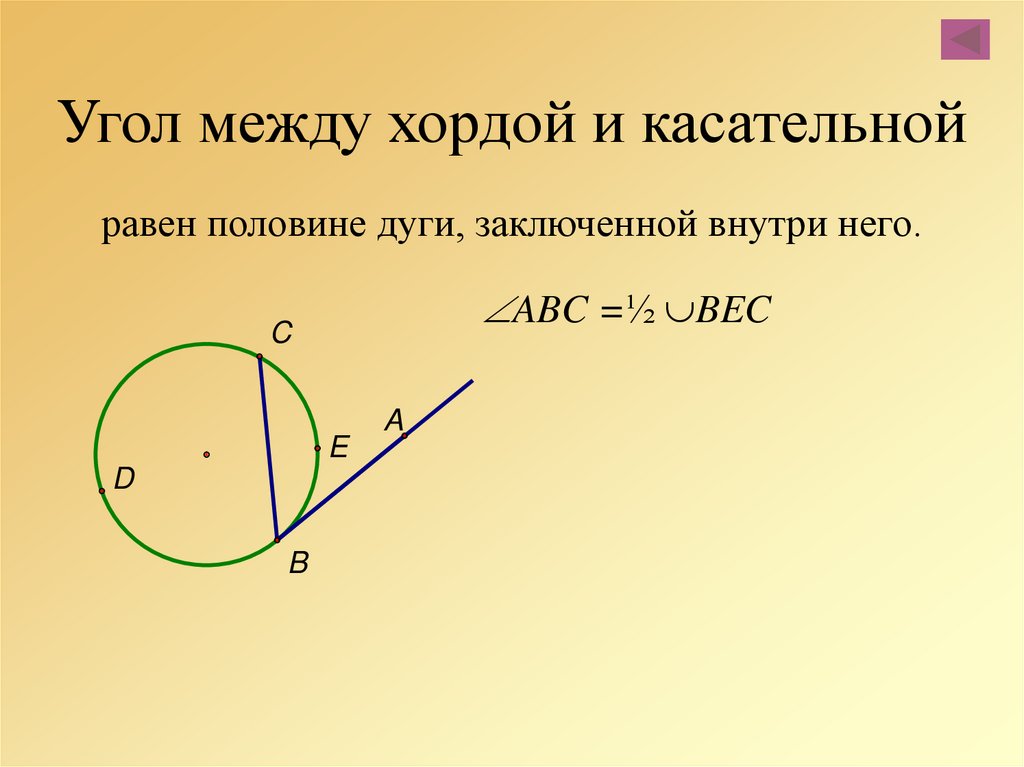
Рассмотрим случай, когда хорда AB проходит именно через точку касания B касательной BC. Тогда по теореме угол между" касательной и хордой "проведенной в точку касания равен половине заключенной между ними дуги AB.

Это наиболее часто используемый на практике случай, поскольку позволяет легко найти искомый угол через другие элементы окружности - дугу или центральный угол.

Угол между касательной хордой равен вписанному углу

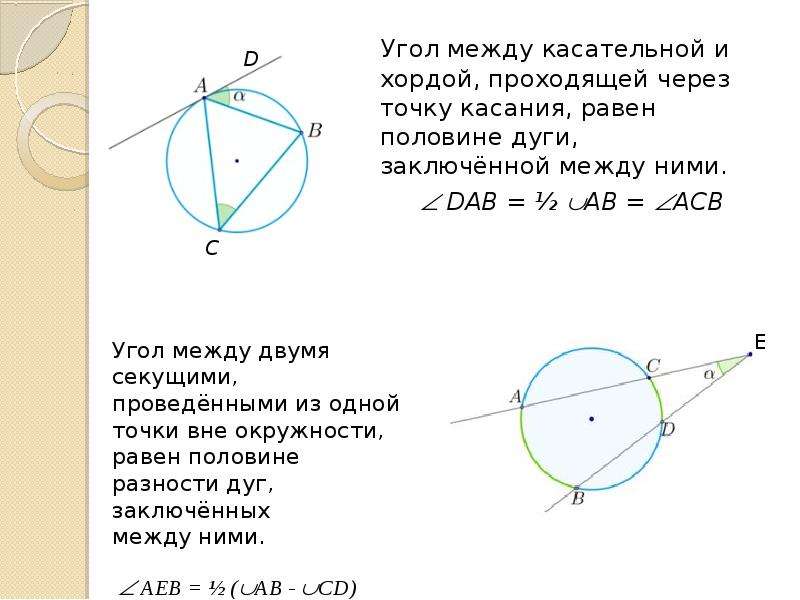
Еще один полезный случай - когда рассматриваемый угол является вписанным (например, угол ACB на рисунке). Тогда он опирается на ту же дугу AB, что и угол между касательной и хордой.

Вписанный угол, как мы знаем, равен половине "своей" дуги. Получается, что вписанный угол ACB равен углу ABC.

Нахождение хорды по известному углу

А что если нужно обратное - найти длину хорды или радиус окружности по известному углу между хордой и касательной?

Это тоже возможно благодаря рассмотренным выше формулам. Давайте разберем такой случай...

Пример задачи на нахождение хорды по углу

Дано: ∠ABC = 30°, AC - радиус окружности, AC = 5 см.

Найти: длину хорды AB.

Решение:

1. ∠ABC - угол между касательной BC и хордой AB.
2. По теореме: ∠ABC = 0,5 * AB (в градусах).
3. Выражаем дугу AB: AB = 2 * ∠ABC = 2 * 30° = 60°.
4. Длина дуги AB равна (60°/360°) * 2πR = (60°/360°) * 2 * 3,14 * 5 см = 5 см.
5. Радиус OC делит хорду AB пополам. Значит, искомая длина AB = 2 * OC = 2 * 5 см = 10 см.

Доказательство. Касательная перпендикулярна радиусу, проведенному в точку касания. Ответ: длина хорды AB = 10 см.

Напомним: Угол между касательной и хордой, проведенной через точку касания, равен половине угловой величины дуги, заключенной между ними. Угол между касательной и хордой является вырожденным случаем вписанного угла, в котором вершина угла совпадает с одним из концов дуги.

Как избежать типичных ошибок

Несмотря на кажущуюся простоту формул, на практике часто допускаются ошибки. Главные из них:

• путание хорды и касательной;
• ошибки при определении знака угла;
• неверный порядок действий в формулах.

Чтобы их избежать, рекомендуется помнить, что так как угол между касательной и хордой равен половине дуги, которую стягивает данная хорда, то и вписанный угол, опирающийся на общую с хордой дугу, также равен половине этой дуги. Следовательно, угол между касательной и хордой равен вписанному углу, который опирается на одну дугу с хордой

Интересные и нестандартные задачи

В заключение приведем несколько необычных задач, которые показывают широкие возможности применения теоремы.

Задача 1

Имеется окружность с центром в точке O и обозначенным на рисунке элементом. Требуется доказать, что если известен угол ABC и радиус окружности, то можно найти расстояние от центра O до точки B.

Решение:

1. По теореме: угол ABC равен половине дуги AB.
2. Дуга AB выражается через радиус R и центральный угол AOB.
3. Центральный угол AOB определяется по теореме косинусов через элементы треугольника AOB.
4. Подставляя R и найденный угол AOB в формулы, получаем расстояние OB.

Ответ: доказано, что расстояние OB можно найти через заданные угол ABC и радиус R.

Задача 2

Дана окружность и точка K вне ее. Известно расстояние от K до центра окружности и до некоторой точки A на окружности. Требуется определить угол между касательной в точке A и хордой AK.

Решение:

1. По теореме косинусов находим радиус окружности через заданные расстояния.
2. Определяем длину хорды AK.
3. Находим дугу, стягиваемую хордой AK.
4. По теореме о хорде и касательной получаем искомый угол.

Ответ: угол найден через заданные расстояния.

Задача 3

Имеется угол, образованный хордой и касательной к окружности радиуса R. Найти площадь круга, вписанного в сектор, образованный рассматриваемым углом.

Решение задачи 3

Дано: R - радиус окружности; α - угол между хордой и касательной.

Найти: S - площадь круга, вписанного в сектор, образованный углом α.

1. По теореме: α = 0,5 * AB, где AB - дуга, заключенная между хордой и касательной.
2. Выражаем дугу AB через центральный угол: AB = 2 * α.
3. Центральный угол равен градусной мере сектора.
4. Находим отношение градусной меры сектора к 360°.
5. Определяем площадь круга: S = πR2.
6. Умножаем S на найденное отношение.

Ответ: площадь круга найдена через радиус R и угол α.