Свойства углов параллелограмма: интересные и полезные факты

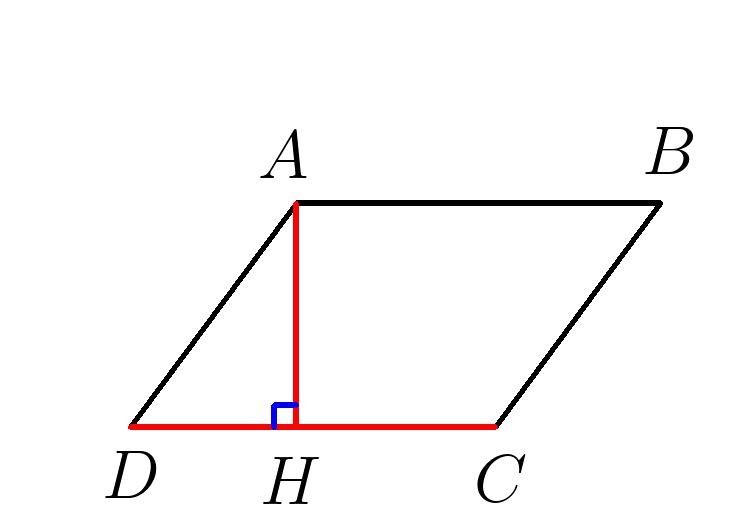
Параллелограмм хранит в себе удивительные свойства, особенно если речь идет об углах этой геометрической фигуры. Давайте попробуем разгадать одну из загадок параллелограмма и узнаем что-то новое об этом интересном четырехугольнике.

Основные свойства параллелограмма и его углов

Итак, дадим определение: параллелограмм - это четырехугольник, у которого противоположные стороны попарно параллельны. У этой фигуры есть несколько важных свойств:

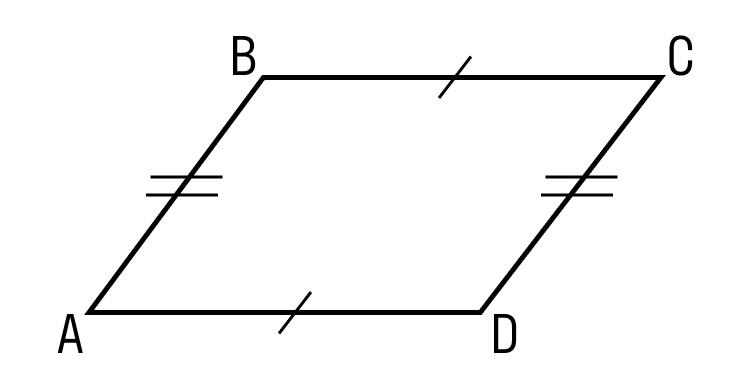
• Противоположные стороны равны
• Противоположные углы равны

Особенно интересно посмотреть на углы параллелограмма. Во-первых, сумма углов, прилежащих к одной стороне, всегда будет равна 180°. Это следует из того, что они являются внутренними односторонними углами при параллельных прямых.

Во-вторых, противоположные углы параллелограмма всегда будут равны друг другу. Это легко доказать с помощью диагоналей, которые делят параллелограмм на два равных треугольника с общим основанием.

Как найти углы параллелограмма

Теперь давайте разберемся, как можно найти углы параллелограмма, если известна какая-то дополнительная информация о них. Рассмотрим несколько вариантов:

Соотношение между углами

Если задано какое-то соотношение между углами (например, один угол в 2 раза больше другого), то можно воспользоваться методом подстановки. Обозначим один угол через x, тогда второй будет равен 2x. Используем свойство суммы углов, прилежащих к одной стороне:

Отсюда находим x = 60°, значит первый угол = 60°, второй = 120°. Таким образом определяем все углы параллелограмма, зная их соотношение.

Теорема косинусов

Если даны стороны параллелограмма и его диагональ, то углы можно найти с помощью теоремы косинусов.

Ее следствие:

Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.

Другие ситуации

Также возможны другие условия задачи - например, может быть известна сумма каких-то двух углов параллелограмма (чаще всего речь идет о противоположных углах). В этом случае также применяются основные свойства параллелограмма: Сумма градусов всех углов равна 360 - для нахождения остальных углов.

Как видите, задачи на нахождение углов параллелограмма решаются достаточно просто, главное правильно использовать его свойства!

Биссектриса параллелограмма

Еще один интересный элемент параллелограмма - это его биссектриса. Биссектрисой называется луч, выходящий из вершины угла и делящий этот угол пополам.

У биссектрисы параллелограмма есть удивительное свойство - она всегда делит противоположную сторону ровно пополам!

Применение биссектрисы

Биссектрису параллелограмма часто используют при решении различных задач. Например, если нужно найти углы параллелограмма, имея информацию о биссектрисах.

Также иногда просят доказать, что четырехугольник является параллелограммом, если известно про биссектрисы. В этом случае применяется описанное выше свойство биссектрисы делить противоположную сторону пополам.

Как видите, даже такой простой элемент как биссектриса имеет удивительные особенности в параллелограмме. Эта тема определенно заслуживает отдельного и более подробного изучения!

В этой статье мы разобрали удивительные свойства углов параллелограмма и ответили на такие вопросы: как найти углы параллелограмма, зная их соотношение или другую информацию о сторонах и диагоналях? Что представляет собой биссектриса параллелограмма и где ее можно применить? Также вы узнаете много интересных и полезных фактов об этом загадочном четырехугольнике.