Гиперболы формула: интересные факты и свойства

Гипербола является одной из самых загадочных и интересных кривых в геометрии. На протяжении веков ее удивительные свойства привлекали внимание величайших математиков. Гипербола обладает элегантной формулой, связывающей расстояния от произвольной точки до двух фиксированных точек. Эта формула позволяет строить потрясающие по красоте кривые с симметричными ветвями. В данной статье мы погрузимся в мир гипербол и откроем некоторые интересные факты об этой загадочной кривой.

История открытия гиперболы

Гипербола была впервые описана древнегреческим математиком Аполлонием Пергским примерно в 262 году до н.э. Он дал ей такое название, поскольку задача о построении точки гиперболы сводилась к "задаче о приложении с избытком". То есть для построения точки использовалось "избыточное" расстояние.

Аполлоний Пергский считается одним из величайших математиков древности. Он написал знаменитый трактат "Конические сечения", полностью посвященный изучению эллипсов, парабол и гипербол. Именно там впервые было строго доказано, что гипербола является сечением конуса плоскостью.

Пример приведения уравнения гиперболы к каноническому виду

Рассмотрим гиперболу, заданную уравнением:

9x^2 - 4y^2 - 36x - 72y + 324 = 0

Чтобы привести его к каноническому уравнению гиперболы, выполним следующие шаги:

1. Перенесем все члены в одну часть уравнения:
2. Разделим переменные x и y на коэффициенты при квадратах:
3. Сгруппируем подобные члены:

В результате получим каноническое уравнение гиперболы с полуосями 3 и 2. Таким образом, зная формулу гиперболы, можно приводить произвольные уравнения гипербол к стандартному каноническому виду.

Нахождение фокусов гиперболы

Одним из важнейших свойств гиперболы формула является постоянство разности расстояний от любой точки гиперболы до двух фиксированных точек - фокусов F1 и F2. Давайте разберемся, как найти вершины гиперболы формула зная положение этих фокусов.

График функции гиперболы

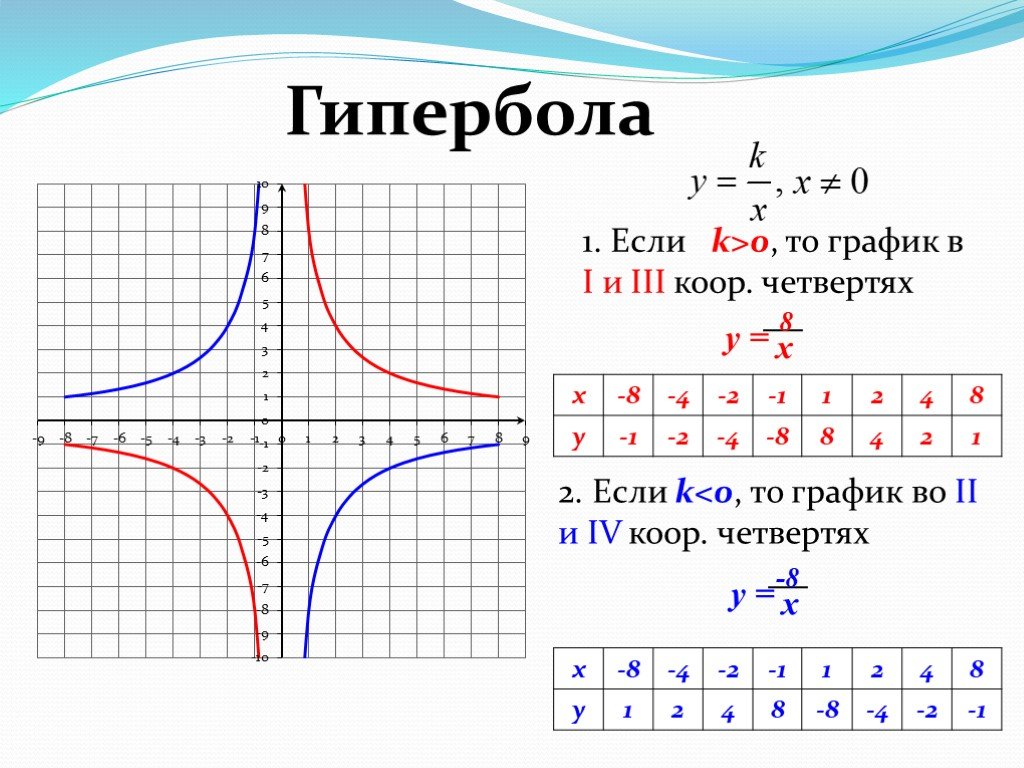
Гипербола также может быть задана как график обратной функции вида y = k/x. Такая функция гиперболы формула имеет две симметричные ветви, уходящие в бесконечность.

Гипербола в архитектуре и технике

Благодаря своим уникальным свойствам гипербола нашла широкое применение в архитектуре, строительстве мостов, конструировании антенн и других областях. Рассмотрим несколько ярких примеров.

В заключение приведем пару любопытных фактов о гиперболах, которые приятно удивят.

Пример функции гиперболы

Рассмотрим функцию вида y = 3/x. Построим ее график:

Мы видим классическую гиперболу с двумя ветвями, уходящими к осям координат. Подставляя различные значения x в формулу функции, можно найти соответствующие точки графика.

Построение графика функции гиперболы

Для построения графика функции гиперболы необходимо:

• Задаться видом функции y = k/x
• Определить значение параметра k и знак
• Построить асимптоты в соответствии со знаком k
• Подобрать несколько точек и нанести их на график
• Соединить точки плавной кривой

Гипербола как модель реальных процессов

Благодаря своему виду график гиперболы часто используется для моделирования различных физических и экономических процессов, таких как теплопередача, разряд конденсатора, спрос и предложение на рынке.

Интересные факты о гиперболе

В заключение приведем несколько любопытных фактов об этой удивительной кривой:

• Траектории движения планет вокруг Солнца описываются уравнениями, близкими к гиперболе
• Форма беговых дорожек на стадионах очень похожа на гиперболу
• Своды и арки многих архитектурных сооружений имеют форму гиперболы

Применение гиперболы в архитектуре

Одной из наиболее интересных областей применения гиперболы является архитектура. Рассмотрим несколько потрясающих примеров использования свойств этой кривой при проектировании зданий и сооружений.

Гиперболические конструкции

Благодаря высокой прочности на растяжение, гипербола формула часто используется при возведении арок, сводов и куполов. Такие гиперболические конструкции обладают повышенной устойчивостью и могут перекрывать большие пролеты.

Гиперболоидные сооружения

Если вращать гиперболу вокруг одной из осей, получится поверхность, называемая гиперболоид вращения. Она также находит широкое применение в строительстве башен, маяков и других сооружений.

Гиперболические башни

Одним из наиболее ярких архитектурных объектов, основанных на формуле гиперболы, является знаменитая башня в Пизе. Ее отклонение от вертикали именно гиперболическое. Это придает уникальный шарм всему сооружению.

Гипербола в физике и технике

Кроме архитектуры гиперболы нашли широкое применение в таких областях как физика, радиотехника, оптика. Рассмотрим несколько конкретных случаев.

Движение планет по гиперболам

Как выяснилось, траектории движения планет вокруг Солнца очень близки к гиперболе. Это позволяет точно рассчитывать их положение в любой момент времени.