Пустое множество: что это такое и зачем оно нужно?

Пустое множество является одним из фундаментальных понятий в математике. Несмотря на кажущуюся простоту, оно играет важную роль в теории множеств и математическом анализе.

Определение пустого множества

Пустое множество – это множество, не содержащее ни одного элемента. Обозначается пустое множество символом ∅.

Например, рассмотрим множество A:

A = {x | x – нечетное число, большее 100}

Очевидно, что таких чисел не существует, следовательно, это множество пусто. Формально:

∅ = {}

Названия пустых множеств

Поскольку пустое множество не имеет элементов, придумать ему осмысленное название не представляется возможным. Любое название будет либо абсурдным («множество круглых квадратов»), либо формальным обозначением (∅).

Свойства пустого множества

Несмотря на кажущуюся тривиальность, у пустого множества есть несколько важных свойств:

1. Пустое множество является подмножеством любого множества
2. Пересечение любого множества с пустым множеством равно пустому множеству
3. Объединение любого множества с пустым множеством равно исходному множеству

Эти свойства пустого множества широко используются в доказательствах в математическом анализе и теории множеств.

Применение пустого множества

Пустое множество применяется:

• В качестве начального элемента при рекурсивных определениях
• Для обозначения невозможного события в теории вероятностей (вероятность пустого множества равна 0)
• В теоретико-множественных формулировках утверждений «ни один», «не существует»

Кроме того, понятие пустого множества используется при изучении алгебраических структур - в частности, при введении понятия нуля в различных алгебраических системах.

Таким образом, несмотря на простоту, пустое множество является фундаментальным объектом, широко применяемым в различных областях математики.

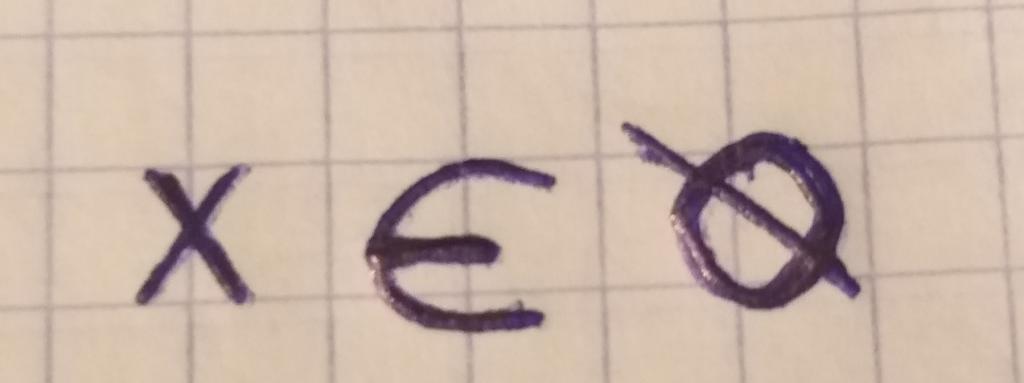
Любопытные факты о пустом множестве

• Пустое множество имеет ровно одно подмножество – само себя: ∅ ⊆ ∅
• Мощность пустого множества равна нулю: |∅| = 0
• Интересный парадокс: множество всех множеств не может содержать само себя, но может содержать пустое множество

Пустое множество в математическом анализе

В математическом анализе пустое множество используется при доказательствах существования пределов. Например, чтобы доказать, что предел последовательности равен L, достаточно показать, что множество точек, в которых последовательность отличается от L больше чем на epsilon, является пустым при любом положительном epsilon.

Пустое множество и рекурсия

Пустое множество часто используется в качестве начального элемента при рекурсивных определениях. Например, множество натуральных чисел можно определить так:

N = {0} ∪ {x+1 | x ∈ N}

Здесь в качестве начального элемента выступает пустое множество {0}.

Пустое множество в теории графов

В теории графов пустое множество соответствует пустому графу – графу без вершин и ребер. Пустой граф обозначается символом ∅ и также обладает некоторыми интересными свойствами.

Аксиома пустого множества

Существует аксиома пустого множества, которая является одной из аксиом Цермело-Френкеля, используемых в аксиоматической теории множеств:

Существует множество ∅, не имеющее элементов.

Эта аксиома гарантирует существование пустого множества в рамках аксиоматики.

Пустое множество в программировании

В языках программирования пустое множество может представляться с помощью пустого массива, списка или другой структуры данных. Работа с пустыми структурами данных также имеет свои особенности, которые должны учитываться при написании алгоритмов.

Построение множеств с помощью пустого множества

Используя пустое множество в качестве начального элемента, можно рекурсивно строить более сложные множества. Например, множество целых чисел:

1. Z = {0} ∪ {x+1 | x ∈ Z} ∪ {x-1 | x ∈ Z}

Здесь сначала определяется {0}, затем используя рекурсию добавляются все положительные и отрицательные целые числа.

Пустое множество и мощность множеств

Мощность пустого множества равна нулю. Мощность объединения двух множеств равна сумме их мощностей за вычетом общих элементов. Из этого следует, что при объединении множества с пустым мощность не изменяется.

Декартово произведение и пустое множество

Декартово произведение любого множества с пустым множеством также является пустым множеством. Это следует из определения декартова произведения и отсутствия элементов в пустом множестве.

Пустое множество в топологии

В топологии существует понятие пустого топологического пространства, которое содержит только одно открытое множество - пустое множество. Такое пространство обозначается ∅ и обладает тривиальной топологией.

Аксиома выбора и пустое множество

Из аксиомы выбора следует, что для пустого множества существует функция выбора (отображение в пустое множество). Это неочевидный результат, поскольку выбрать элемент из пустого множества невозможно.

Пустое множество и частично упорядоченные множества

В теории частично упорядоченных множеств пустое множество является наименьшим элементом. Любой элемент частично упорядоченного множества больше любого элемента пустого множества.

Пустое множество как начальное при обучении

При обучении математике понятие пустого множества вводится в качестве простейшего примера множества. Это позволяет интуитивно объяснить что такое множество и какими свойствами оно обладает.

Пустое множество в математических шутках

Иногда пустое множество используется в математическом юморе и шутках. Например: «Сколько математиков нужно, чтобы вкрутить лампочку? Один, остальные преобразуют пустое множество».

Несчетность пустого множества

Хотя пустое множество не имеет элементов, оно все же является несчетным множеством. Это следует из теоретико-множественного определения счетности.

Обобщения пустого множества

Существуют обобщения пустого множества, например, понятие начального объекта в категориях. Такой начальный объект обобщает некоторые свойства пустого множества на произвольные категории.