Неравенство Бернулли: история открытия и применение в математике

Неравенство Бернулли является одним из фундаментальных результатов математического анализа. Оно позволяет сравнивать показательные и степенные функции с линейными. Это открытие швейцарского математика Якоба Бернулли в конце XVII века значительно продвинуло науку вперед.

История открытия неравенства Бернулли

Якоб Бернулли (1654-1705) — выдающийся математик, один из основателей теории вероятностей. Он родился в семье аптекаря в Швейцарии и с детства проявлял незаурядные математические способности.

В 1689 году Бернулли опубликовал трактат, в котором впервые сформулировал и доказал неравенство, носящее ныне его имя. Это неравенство Бернулли утверждает:

При любом натуральном n и любом x > -1 выполняется неравенство:

(1 + x)ⁿ ≥ 1 + nx

Неравенство Бернулли позволяет оценивать степенную функцию снизу линейной. Доказательство Бернулли основано на методе математической индукции. Рассмотрим его подробнее.

1. База индукции. При n = 1 неравенство выполняется как равенство.
2. Предположение индукции. Допустим неравенство верно для некоторого n.
3. Переход. Докажем, что тогда оно верно и для n+1. Перемножаем обе части на (1+x) и получаем требуемый результат.

Интересный факт, Якоб Бернулли изначально сформулировал это неравенство лишь для натуральных показателей степени. Его брат Иоганн Бернулли (тоже известный математик) в 1694 году обобщил это неравенство на действительные и комплексные числа.

Обобщенная форма неравенства Бернулли

Помимо классического вида, существует обобщенная форма неравенства Бернулли:

Пусть x₁, x₂,..., x_n - числа одного знака, большие -1. Тогда выполняется:

(1 + x₁)(1 + x₂)...(1 + x_n) ≥ 1 + x₁ + x₂ + ... + x_n

Это обобщенное неравенство можно доказать по аналогии с методом Бернулли - математической индукцией. Ключевая идея та же - перемножить обе части на положительный множитель.

Основное отличие обобщенной формы в том, что она применима не только для целых степеней, но и для произвольных произведений скобок вида (1 + x). Это расширяет область применения неравенства Бернулли для сложных математических выкладок.

Применение в теории вероятностей

Неравенство Бернулли тесно связано с теорией вероятностей. Рассмотрим классическую схему Бернулли - повторение независимых испытаний с вероятностью успеха в каждом испытании, равной p. Тогда неравенство Бернулли позволяет оценить вероятность получить ровно k успехов за n испытаний.

Это применяется, к примеру, при доказательстве теоремы Пуассона, устанавливающей сходимость биномиального распределения к пуассоновскому. Неравенство Бернулли используется для получения оценок, необходимых в этом доказательстве.

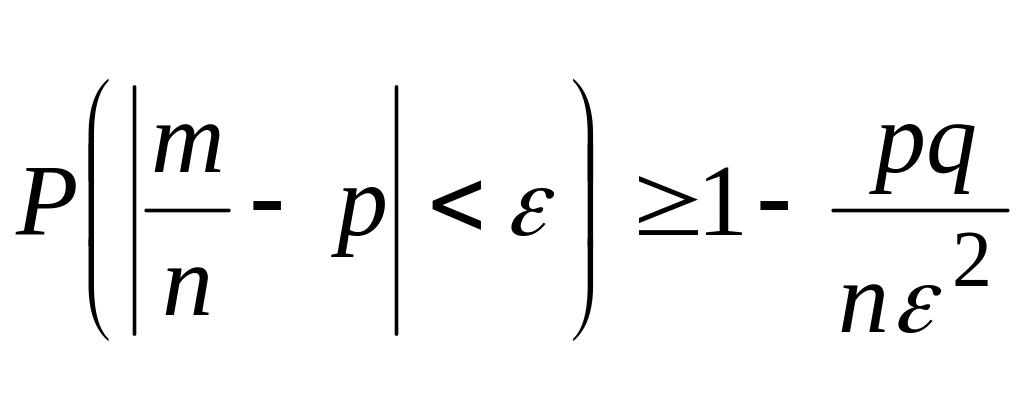
Рассмотрим классическую задачу. Имеется 100 независимых испытаний, в каждом из которых вероятность успеха равна 0.01. Требуется оценить вероятность получить хотя бы один успех. Решение основано как раз на неравенстве Бернулли с натуральным показателем степени.

Для решения этой задачи применим неравенство Бернулли. Пусть p = 0.01 - вероятность успеха в одном испытании, тогда вероятность неудачи в одном испытании равна q = 1 - p = 0.99. Вероятность хотя бы одного успеха за 100 испытаний равна 1 минус вероятность 100 неудач:

P(хотя бы 1 успех за 100 испытаний) = 1 - P(100 неудач) = 1 - q¹⁰⁰

Применим неравенство Бернулли для оценки степени q¹⁰⁰ снизу:

q¹⁰⁰ ≥ 1 - 100q

Подставляя значение q = 0.99, получаем:

P(хотя бы 1 успех) ≥ 1 - 0.36 = 0.64

Другие примеры из теории вероятностей

Рассмотрим еще несколько примеров применения неравенства Бернулли в теории вероятностей и статистике:

• Доказательство неравенства Чебышева для суммы независимых случайных величин
• Оценка хвостов распределения в предельных теоремах
• Доказательство закона больших чисел в форме Бернулли
• Обоснование метода максимального правдоподобия в статистике

Критерий проверки гипотез с помощью неравенства Бернулли

Еще одно важное применение неравенства Бернулли в статистике — это критерий проверки статистических гипотез. Рассмотрим суть на примере.

Пусть выдвинута нулевая гипотеза H0 о том, что вероятность наступления некоторого события в испытаниях равна p0. Проводится n независимых испытаний, в результате которых событие наступило k раз. Необходимо проверить, согласуются ли эти данные с гипотезой H0.

Применение неравенства Бернулли в анализе и дифференциальном исчислении

Помимо теории вероятностей, неравенство Бернулли широко используется в математическом анализе для доказательства свойств функций.

Вывод свойств показательной функции

Одно из основных применений — это вывод свойств показательной функции и неравенство Бернулли используется в следующих доказательствах:

• Монотонность показательной функции
• Выпуклость показательной функции
• Нахождение асимптот показательной функции