Самый простой способ решения систем уравнений с двумя неизвестными за 5 минут

Решить систему двух линейных уравнений с двумя неизвестными действительно можно всего за 5 минут, если знать простой и понятный алгоритм. Давайте разберемся!

Что такое система уравнений и зачем ее решать

Системой уравнений называют совокупность двух или больше уравнений, решаемых относительно двух или больше переменных. Например:

• 2x + 3y = 12
• 4x - 5y = 13

Здесь два уравнения решаются относительно двух неизвестных x и y.

Зачем нужно уметь решать системы уравнений? Во-первых, они часто встречаются в различных практических задачах - физических, химических, экономических. Во-вторых, этот навык полезен для развития логического и аналитического мышления.

Первые системы уравнений стали решать еще в Древнем Египте при расчетах урожайности полей после разлива Нила. Но основы современной теории были заложены лишь в 17-18 веках в трудах математиков Р. Декарта и Л. Эйлера.

Основные способы решения систем уравнений

Решение систем уравнений с двумя неизвестными можно осуществлять четырьмя способами:

1. Метод подстановки
2. Метод сложения
3. Графический метод
4. Метод введения новых переменных

Рассмотрим их по порядку.

Метод подстановки

Суть метода: одну неизвестную выражаем через другую из одного уравнения и подставляем во второе уравнение:

• Из уравнения 2x + 3y = 12 выразим y = (12 - 2x)/3
• Подставим это выражение в уравнение 4x - 5y = 13
• Получим уравнение только с одной переменной x, решаем его
• Находим значение y, подставляя x в первоначальную формулу для y

Этот классический метод хорошо всем известен, но не всегда удобен на практике из-за громоздких преобразований.

Метод сложения

Суть: умножаем уравнения системы на такие числа, чтобы при сложении уравнений одна из переменных "исчезла". Остается уравнение с одной переменной, его решаем.

Например, в системе:

• 2x + 3y = 12
• 4x - 5y = 13

Умножим первое уравнение на -4, второе - на 2. При сложении получим уравнение с одной переменной y:

• -8x - 12y = -48
• 8x - 10y = 26
• -22y = -22
• y = 1

Далее находим x, подставляя значение y в одно из исходных уравнений системы.

Этот метод чуть проще в использовании, чем метод подстановки.

Решение систем уравнений с двумя неизвестными графическим способом

Графический метод основан на построении графиков обоих уравнений системы на координатной плоскости. Точка пересечения этих графиков и будет искомым решением системы.

Удобен для приближенных вычислений, нагляден. Но применим только для систем с двумя уравнениями и двумя неизвестными.

Пошаговая инструкция самого простого способа

Самым простым способом решения системы двух линейных уравнений является метод сложения. Давайте рассмотрим его пошагово.

1. Записываем систему уравнений, которую нужно решить
2. Умножаем оба уравнения системы на такие числа, чтобы при сложении уравнений одна из переменных \"исчезла\"
3. Складываем уравнения и решаем полученное уравнение с одной неизвестной
4. Находим вторую переменную, подставляя найденное значение в одно из исходных уравнений системы
5. Записываем ответ - найденные значения обеих переменных x и y

Теперь давайте опробуем этот алгоритм в действии.

Иллюстрирующий числовой пример

Решим систему уравнений методом сложения:

• 2x + 3y = 12
• 4x - 5y = 13

1. Умножим первое уравнение на -4, второе на 2:

• -8x - 12y = -48
• 8x - 10y = 26

1. Сложим уравнения:
   -22y = -22 y = 1
2. Найдем x, подставив y = 1 в первое уравнение: 2x + 3·1 = 12 2x = 9 x = 4,5

Ответ: x = 4,5; y = 1.

На все ушло 3 минуты! Действительно, этот самый простой алгоритм позволяет быстро решить систему уравнений с двумя неизвестными.

Рекомендации по применению метода

Чтобы научиться решать системы уравнений за 5 минут, полезно выполнить несколько упражнений самостоятельно. Вот несколько советов для закрепления навыка:

• Начните с простых систем из двух линейных уравнений
• Старайтесь решать \"в уме\", без записи промежуточных преобразований
• Засекайте время выполнения каждой системы, сравнивайте со временем в 5 минут
• Применяйте метод сложения как можно чаще, это позволит довести его использование до автоматизма

Вот несколько примеров систем уравнений для самостоятельного решения систем уравнений с двумя неизвестными:

Графический способ решения систем уравнений

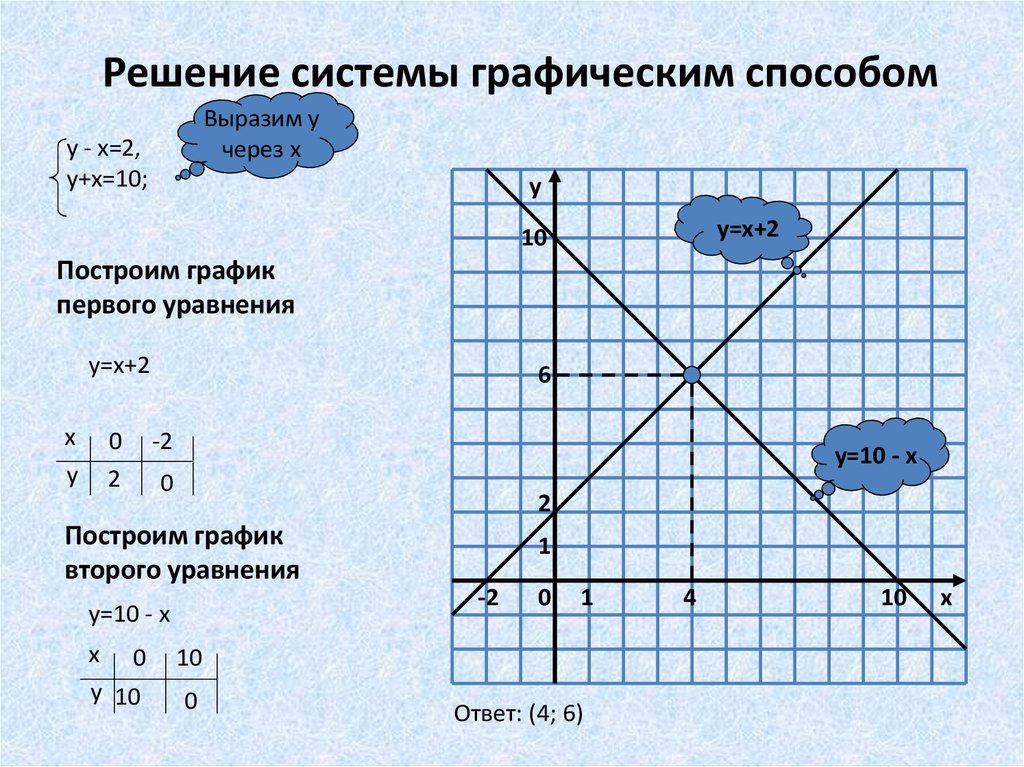
Рассмотрим подробнее графический метод решения систем линейных уравнений с двумя неизвестными. Его суть заключается в следующем:

1. Строим на координатной плоскости график каждого уравнения системы
2. Находим точку пересечения полученных графиков
3. Координаты точки пересечения и будут искомым решением системы уравнений

Рассмотрим числовой пример:

Дана система:

• 2x + 3y = 12
• 4x - 5y = 13

1) Строим график первого уравнения. Приравняем его к 0:

2x + 3y - 12 = 0

Получаем прямую линию с угловым коэффициентом k = -2/3.

2) Аналогично строим график второго уравнения:

4x - 5y - 13 = 0

Получаем прямую линию с угловым коэффициентом k = 4/5.

3) Определяем точку пересечения графиков. Ее координаты x = 4,5; y = 1.

Это и есть искомое решение системы уравнений, найденное графическим способом.

Достоинства графического метода

• Наглядность и простота построения графиков
• Возможность найти приближенное решение
• Полезен для проверки решений, найденных аналитически

Недостатки графического метода

• Трудоемкость вычислений координат точек для построения графиков
• Невозможность построить график для систем более чем из двух уравнений
• Погрешность при нахождении координат точки пересечения визуально

Таким образом, графический способ решения систем уравнений с двумя неизвестными полезен в ряде случаев, но имеет и определенные ограничения.

Использование систем уравнений в практических задачах

Где в реальной жизни можно столкнуться с необходимостью построить и решить систему уравнений? Рассмотрим несколько примеров.

Задачи по физике

Системы уравнений часто возникают при решении физических задач на движение двух тел, взаимодействие сил, определение характеристик электрических цепей и т.д.

Например, два автомобиля выехали навстречу друг другу из пунктов А и В, находящихся на расстоянии 360 км. Скорость первого авто 60 км/ч, второго - 40 км/ч. Через какое время они встретятся?

Здесь записывается система из двух уравнений относительно двух неизвестных - времени t и расстояния s от точки А:

• s = 60t (уравнение движения первого авто)
• 360 - s = 40t (второго авто)

Задачи по химии

При решении задач на нахождение массовой или объемной доли компонентов в смесях также приходится составлять и решать системы уравнений.

Например, сколько литров 5% раствора серной кислоты и сколько литров 10% раствора этой же кислоты нужно взять для приготовления 8 л 8%-ного раствора?

Составляем систему уравнений относительно объемов двух растворов V₁ и V₂ :

• 0,05V₁ + 0,1V₂ = m (уравнение масс)
• V₁ + V₂ = 8 (уравнение объемов)