Теорема о вертикальных углах: всегда ли они равны?

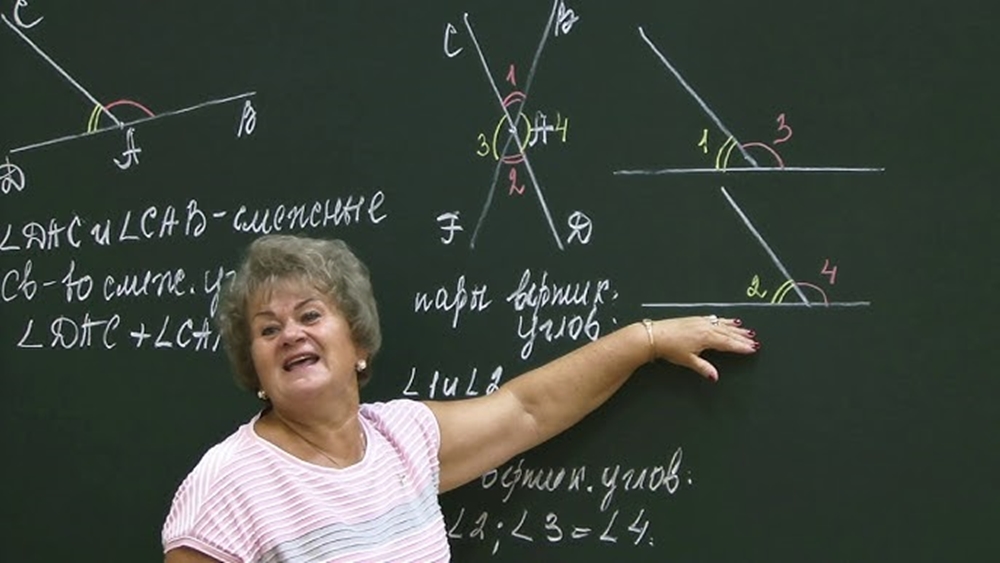
Теорема о вертикальных углах является одной из фундаментальных теорем геометрии. Она утверждает, что вертикальные углы, образованные двумя пересекающимися прямыми, равны друг другу. Эта простая, но мощная теорема имеет множество практических применений в математике, физике и других областях.

Формулировка теоремы

Формально теорему о вертикальных углах можно сформулировать следующим образом:

Если две прямые пересекаются, то вертикальные углы, образованные этими прямыми, равны.

Здесь под вертикальными углами понимаются пары углов, вершины которых лежат на пересечении двух прямых, а стороны являются полупрямыми, выходящими из точки пересечения.

Доказательство теоремы

Существует несколько способов строгого математического доказательства этой теоремы. Рассмотрим одно из наиболее простых и элегантных доказательств с использованием вспомогательных построений.

1. Пусть даны две пересекающиеся прямые AB и CD. Обозначим точку их пересечения буквой O (см. рисунок).
2. Соединим точку O с произвольной точкой M на прямой AB.
3. Из точки M опустим перпендикуляр MP на прямую CD.

Тогда в силу свойств перпендикуляра, углы OMP и OPM являются прямыми. Кроме того, по определению вертикальных углов, углы AOMP и АОПМ также являются вертикальными.

Но тогда, опираясь на базовое свойство прямоугольных треугольников о равенстве острых углов, получаем:

• ∠AOMP = ∠OPM
• ∠АОПМ = ∠OMP

Поскольку выбор точки M был произвольным, это равенство справедливо для любой пары вертикальных углов, образованных прямыми AB и CD. Что и требовалось доказать.

Теорема: вертикальные углы равны

Как видно из приведенного выше доказательства, теорема о вертикальных углах действительно утверждает, что такие углы равны. Это важное свойство используется при решении многих геометрических задач и доказательстве других утверждений.

Следствия из теоремы

Из теоремы о вертикальных углах можно получить несколько важных следствий, широко используемых на практике.

1. Если одна прямая перпендикулярна другой, то она перпендикулярна и к любой прямой, параллельной данной.
2. Если при пересечении двух параллельных прямых секущей соответственные углы равны, то эти прямые параллельны.

Эти и некоторые другие следствия позволяют эффективно оперировать понятием параллельности в геометрических построениях и доказательствах.

Применение теоремы

Теорема о вертикальных углах находит применение для решения множества геометрических задач. Рассмотрим несколько примеров.

1. Нахождение углов в различных конфигурациях треугольников и четырехугольников путем сведения к вертикальным углам.
2. Вычисление высот и медиан в треугольниках, опираясь на равенство вертикальных углов.
3. Доказательство параллельности или перпендикулярности отдельных отрезков в сложных геометрических фигурах.

Кроме геометрических задач, теорема применима и в физике. Например, она используется при изучении законов отражения и преломления света, а также для описания относительного движения объектов в механике.

Обобщения теоремы

Хотя сформулирована теорема для пересечения именно прямых, она справедлива и в более общем случае. А именно, вертикальные углы будут равны также при пересечении:

• Дуг окружностей
• Отрезков кривых (при условии их пересечения под ненулевым углом)
• Плоскостей в пространстве

Эти обобщения позволяют использовать свойство равенства вертикальных углов в более широком классе геометрических объектов.