Векторное произведение векторов: суть, понятия и формула

Векторное произведение - важная математическая операция, позволяющая находить вектор, перпендикулярный двум другим. Эта операция широко используется в физике, технике, графике для решения различных задач. Но не все знают, что означает сам термин "векторное произведение" и как вычислить это произведение для конкретных векторов. Давайте разберемся!

1. Определение векторного произведения векторов

Итак, векторным произведением двух векторов \overrightarrow{a} и \overrightarrow{b} называют вектор \overrightarrow{c}, который:

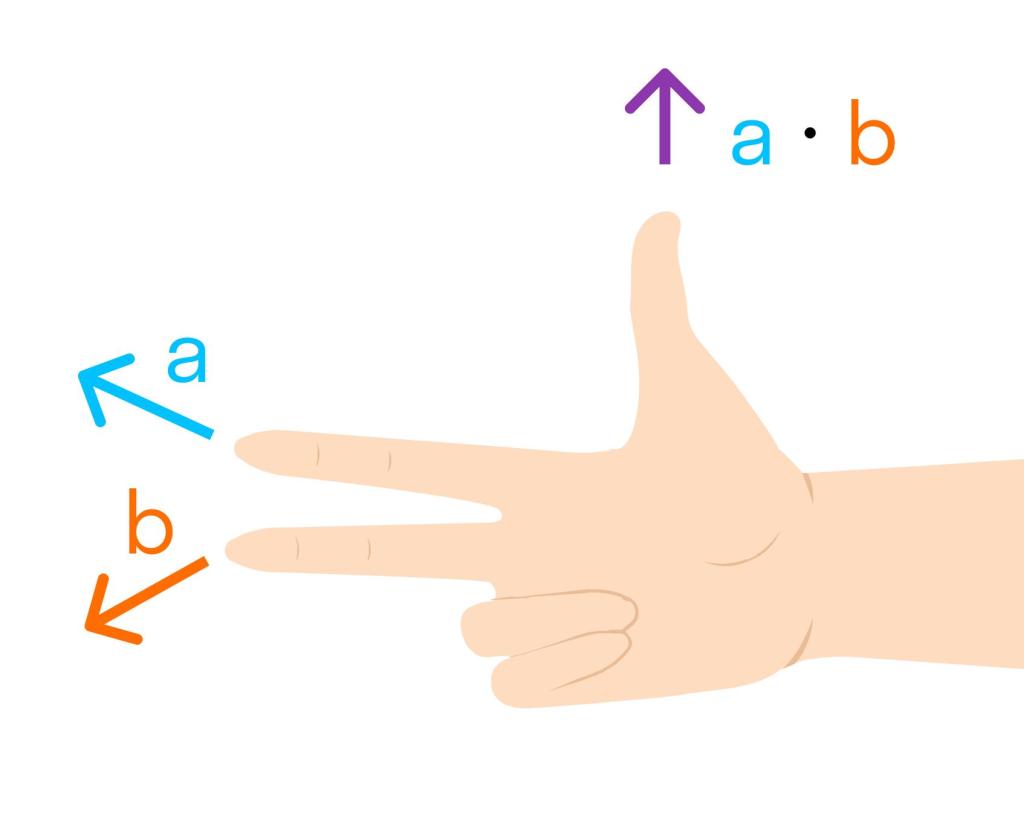
• Направлен перпендикулярно к плоскости, образованной векторами \overrightarrow{a} и \overrightarrow{b}
• Его модуль равен площади параллелограмма, построенного на этих векторах
• Он образует с \overrightarrow{a} и \overrightarrow{b} правую тройку векторов

То есть векторное произведение позволяет получить вектор, перпендикулярный двум заданным. Это его основное отличие от скалярного произведения, которое дает скаляр (число).

2. Вычисление векторного произведения векторов

Для вычисления векторного произведения векторов \overrightarrow{a} и \overrightarrow{b} используется формула:

\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b} = |i \quad j \quad k|
|a_x \quad a_y \quad a_z| |b_x \quad b_y \quad b_z|

Где a_x, a_y, a_z - координаты вектора \overrightarrow{a}, а b_x, b_y, b_z - координаты вектора \overrightarrow{b}. Получаемый вектор \overrightarrow{c} имеет координаты:

• c_x = a_yb_z - a_zb_y
• c_y = a_zb_x - a_xb_z
• c_z = a_xb_y - a_yb_x

Это и есть основная формула векторного произведения векторов.

Также существуют другие формы записи, например через единичные базисные векторы \overrightarrow{i}, \overrightarrow{j}, \overrightarrow{k} или с помощью матрицы .

3. Геометрические приложения

Векторное произведение часто используется для решения различных геометрических задач. Например, позволяет легко найти:

• Площадь параллелограмма, построенного на векторах \overrightarrow{a} и \overrightarrow{b}:

  S = |\overrightarrow{a} \times \overrightarrow{b}|

• Площадь треугольника по двум его сторонам:

  S = \frac{1}{2}|\overrightarrow{a} \times \overrightarrow{b}|

• Перпендикуляр к плоскости, заданной двумя векторами

То есть векторное произведение является удобным инструментом для вычислений, связанных с перпендикулярностью и площадями фигур в пространстве.

4. Физические приложения

В физике векторное произведение позволяет найти такие важные величины, как:

• Момент силы относительно точки:

  \overrightarrow{M} = \overrightarrow{r} \times \overrightarrow{F}

• Сила Лоренца, действующая на заряженную частицу в магнитном поле:

  \overrightarrow{F} = q(\overrightarrow{v} \times \overrightarrow{B})

• Момент импульса частицы и другие физические величины

Без использования векторного произведения многие важные физические законы и формулы записать было бы невозможно!

В этом и заключается огромная польза векторного произведения векторов - оно позволяет упростить многие вычисления в математике, физике и других областях.

5. Использование в компьютерной графике

Векторное произведение находит применение и в компьютерной графике при моделировании трехмерных сцен и объектов. Например, оно используется для:

• Построения нормалей к поверхностям моделей
• Определения направления освещенности от источников света
• Моделирования различных эффектов вроде отражений и преломлений

Зная нормали к поверхности, можно корректно рассчитать освещение в каждой точке, что важно для реалистичного отображения объектов.

6. Особые случаи

Рассмотрим некоторые частные случаи векторного произведения:

• Если векторы коллинеарны (сонаправлены), то их произведение равно нулю
• Если векторы ортогональны (взаимно перпендикулярны), то модуль их произведения равен произведению модулей самих векторов
• Произведение любого вектора на нулевой вектор дает нулевой же вектор

Эти свойства часто используются при решении задач с векторным произведением.

7. Связь с другими операциями

Помимо перечисленного, векторное произведение тесно связано с другими векторными и скалярными операциями. В частности:

• Оно тесно связано со смешанным произведением векторов
• Позволяет записать условия коллинеарности и компланарности векторов
• Используется в формуле для нахождения расстояния от точки до плоскости
• Связано с определителями матриц через координатный метод

Итак, мы разобрали что такое векторное произведение, его вычисление, основные свойства и применения. Эта операция играет важную роль в математике, физике, инженерии и компьютерной графике. Зная ее сущность, можно решать задачи, связанные с перпендикулярностью векторов, нахождением площадей, моментов сил и других величин.

Практические примеры

Давайте рассмотрим несколько практических примеров применения векторного произведения для решения задач.

Пример 1. Вычисление площади треугольника

Даны векторы сторон треугольника \overrightarrow{a} = (3, 0, -4) и \overrightarrow{b} = (-5, 7, 2). Требуется найти площадь этого треугольника с помощью векторного произведения.

Решение. Площадь треугольника вычисляется по формуле: S = (1/2)|\overrightarrow{a} × \overrightarrow{b}|. Подставляя координаты векторов, получаем: \overrightarrow{a} × \overrightarrow{b} = (3, 21, -14). Его модуль равен 25. Тогда площадь искомого треугольника S = (1/2)·25 = 12,5.

Пример 2. Вычисление момента силы

Даны сила \overrightarrow{F} = (1, 2, -3) Н, приложенная в точке A(2, -1, 4) и точка O(-1, 2, 0), относительно которой нужно найти момент. Вычислить момент силы \overrightarrow{F} относительно точки O.

Решение. Запишем радиус-вектор \overrightarrow{r} от точки O до точки приложения силы: \overrightarrow{r} = (2 - (-1), -1 - 2, 4 - 0) = (3, -3, 4). Тогда искомый момент вычисляется стандартно: \overrightarrow{M} = \overrightarrow{r} × \overrightarrow{F} = (-3, -12, 3) Н·м.

Историческая справка

Векторное произведение было впервые введено в 1843 году ирландским математиком У. Гамильтоном в рамках его работ по кватернионам - числовым системам для описания пространства. Изначально Гамильтон определил векторное произведение именно как часть произведения двух кватернионов.

Позже эта идея была перенесена в векторную алгебру и получила широкое применение в физике и технике. Со временем были открыты многочисленные свойства и особенности векторного произведения, которые мы рассмотрели выше.

В этой статье мы разобрались, что собой представляет векторное произведение, как оно вычисляется и для чего используется на практике. Это фундаментальная математическая операция, играющая важную роль в решении инженерных и научных задач. Знание ее свойств и умение применять для вычислений является обязательным для специалистов многих областей.