Назначение, свойства и особенности оси ординат

Ось ординат является неотъемлемой частью прямоугольной системы координат. Без нее невозможно точно определить положение точки на плоскости.
Определение оси ординат
Прямоугольная система координат, в которой используется ось ординат, была изобретена французским математиком и философом Рене Декартом в 1637 году.
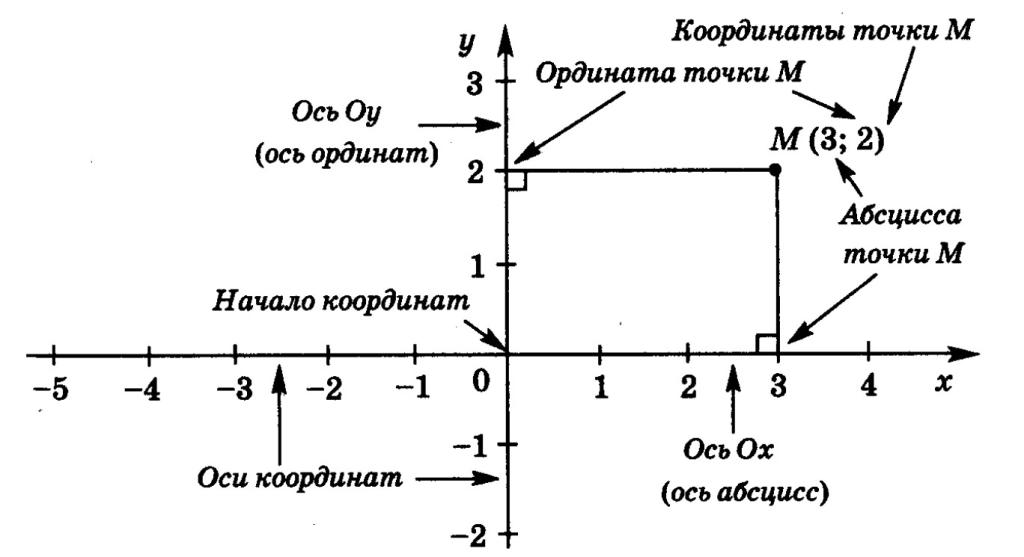
Ось ординат – это одна из двух перпендикулярных координатных осей в прямоугольной системе координат. Обычно ось ординат изображается вертикально.
Ось ординат тесно связана с осью абсцисс – второй горизонтальной осью этой системы координат. Вместе эти оси позволяют однозначно определить положение любой точки на координатной плоскости с помощью двух координат – абсциссы и ординаты.
Назначение оси ординат
Основным назначением оси ординат является определение координат точек на плоскости. Рассмотрим это подробнее.
- Проводим из точки перпендикуляр на ось ординат.
- Определяем длину отрезка от начала координат до точки пересечения с перпендикуляром.
- Эта длина в выбранном масштабе и есть ордината искомой точки.
Зная ординату и соответствующую ей абсциссу, можно точно построить положение любой точки на координатной плоскости. Также по значению ординаты можно определить, в какой из четырех координатных четвертей находится данная точка.
Еще одно важное применение оси ординат – это построение графиков различных функций. На графике функции y=f(x) ось ординат используется для откладывания значений функции y, соответствующих различным значениям аргумента x на оси абсцисс.

Свойства и особенности оси ординат
Ось ординат обладает рядом уникальных свойств, вытекающих из ее математической природы:
- Является проекцией точки на вертикальную ось;
- Отражает «высоту» расположения точки на плоскости;
- Всегда является второй координатой точки после абсциссы;
- Обеспечивает ортогональность системы координат.
Дополнительные особенности оси ординат:
| Масштаб оси ординат | Может быть любым, в зависимости от решаемой задачи |
| Разметка оси ординат | Может быть числовой, буквенной, временной и т.д. |
| Обозначения оси ординат | Традиционно обозначается буквой Y либо y |
Таким образом, ось ординат является важнейшей составляющей прямоугольной системы координат, позволяющей определять положение точек на плоскости и строить различные графики.
Практические рекомендации по использованию оси ординат
Чтобы правильно работать с осью ординат, следует придерживаться нескольких простых рекомендаций:
- При построении оси ординат обязательно соблюдайте ее перпендикулярность оси абсцисс.
- Выбирайте масштаб оси ординат исходя из диапазона значений, которые предполагается на ней откладывать.
- Делайте разметку и подписи на оси ординат таким образом, чтобы было удобно считывать координаты точек.
Построение графиков функций с использованием оси ординат
При построении графика функции y=f(x) на оси ординат откладывается значение переменной y, вычисленное по заданной функции f для различных значений аргумента x. Так для функции y=2x+1 при x=1 значение y=3, которое и откладывается на оси Y на высоте 3 единиц от начала координат.
Интересные факты об оси ординат
- У разных народов в древности существовали свои формы графического представления данных, похожие на современную систему координат.
- Ось ординат часто можно увидеть на инфографике, представляющей различные статистические данные.
Применение оси ординат на практике
Ось ординат используется в самых разных областях:
- Построение графиков в математике, физике, экономике, статистике и других науках
- Описание движения объектов в навигации и картографии
- Представление изменения параметров во времени в различных системах управления
- Отображение данных датчиков, например давления или температуры
Ось ординат в многомерных системах координат
В многомерных системах координат используется несколько осей ординат, по одной на каждое измерение. Например, в трехмерной системе присутствуют три оси ординат - Y, Z и еще одна ось, перпендикулярная им. Это позволяет однозначно описать положение точки в пространстве.
Похожие статьи
- Подготовительная группа по физкультуре: что нельзя делать?
- Зачем нужна география в жизни? Зачем нужно изучать географию?
- Закрыть гештальт - что это? Значение и особенности
- Специальность "государственное и муниципальное управление": кем потом работать?
- Легенда и миф о Зевсе кратко для учащихся 5 класса
- Общая характеристика русской литературы 19 века: описание, особенности и интересные факты
- К чему снятся змеи женщине? Толкование снов
