Симметрия относительно точки: базовые понятия, практические примеры

Центральная симметрия - удивительное свойство некоторых геометрических фигур, которое на первый взгляд кажется очевидным, но таит в себе множество интересных особенностей. Давайте разберемся, что это такое и почему важно.

Основные понятия центральной симметрии

Итак, симметрия относительно точки или центральная симметрия - это такое преобразование фигуры, при котором каждая точка меняется местами со своей симметричной относительно некоторого центра.

Центральная симметрия — это свойство геометрической фигуры, имеющей произвольные точки А и А1, которые соединяют отрезок и совпадают в пространстве относительно фиксированного элемента — центральной точки О.

Центр симметрии - это и есть та самая фиксированная точка О. Часто центр симметрии совпадает с какой-то особой точкой фигуры. Например, для окружности им будет центр окружности, для параллелограмма - точка пересечения диагоналей.

А вот симметричные точки А и А1 удалены от центра О на одинаковое расстояние. Причем О является серединой отрезка АА1. Чтобы найти симметричную точку, достаточно отложить от центра О расстояние, равное ОА, в противоположную от А сторону.

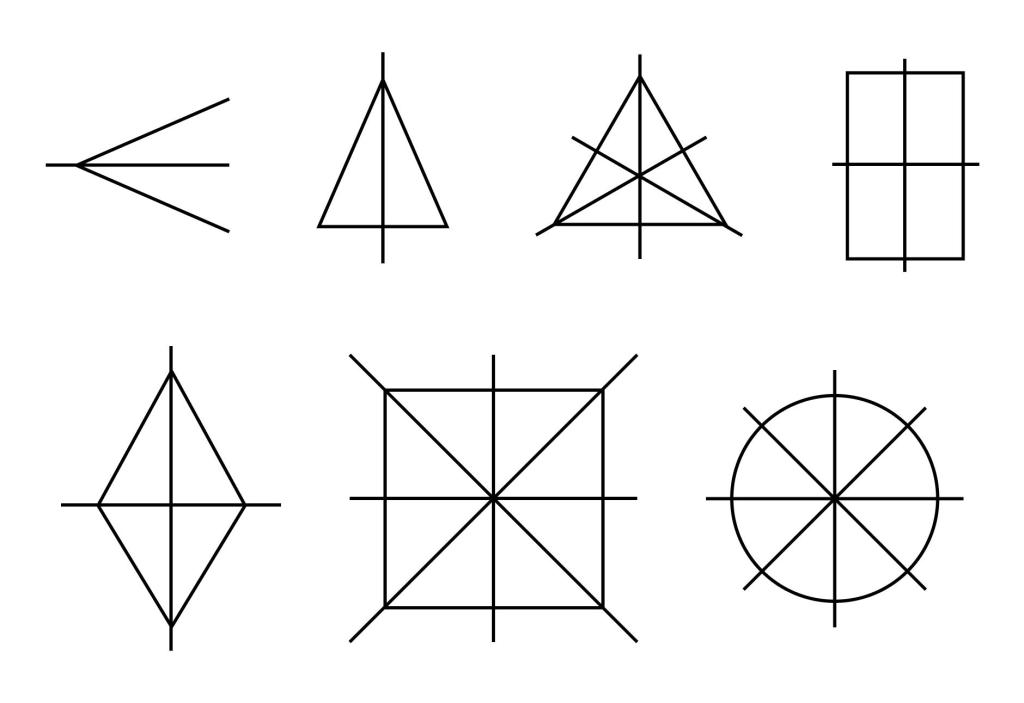
Симметрия относительно точки (примеры) - окружность, правильные многоугольники, параллелограмм, ромб и другие фигуры с осевой или центральной симметрией.

Свойства центрально симметричных фигур

У центральной симметрии есть несколько важных свойств, которые нужно знать:

• Сохраняются расстояния между точками
• Отрезки и лучи переходят в отрезки и лучи
• Параллельные объекты остаются параллельными
• Фигура не меняет площадь и общую форму

Практическое применение

На практике центральная симметрия часто используется в архитектуре, дизайне, живописи. Она позволяет создавать гармоничные композиции, уравновешивая и связывая разные элементы.

Например, симметрия относительно точки (примеры из жизни):

1. Симметричные узоры в оформлении фасадов зданий
2. Орнаменты и бордюры с использованием осевой или центральной симметрии
3. Композиция картины или фотографии относительно оптического центра

Кроме того, многие природные объекты тоже обладают центральной симметрией - снежинки, пчелиные соты, раковины моллюсков и др.

Построение симметричных фигур

Чтобы построить фигуру, симметричную данной относительно точки О, нужно выполнить следующие действия:

1. Соединить каждую вершину (или другую значимую точку) исходной фигуры с центром симметрии О
2. Отложить на каждом из этих отрезков такой же по длине отрезок от точки О, но в противоположную сторону
3. Соединить полученные точки так же, как были соединены вершины исходной фигуры

Центральная симметрия в архитектуре

В архитектуре центральная симметрия часто используется при проектировании различных сооружений - храмов, дворцов, административных зданий. Это придает им монументальность, значимость, подчеркивает их общественное предназначение.

Яркий пример - архитектура Санкт-Петербурга в стиле барокко. Многие здания имеют четкую симметричную планировку относительно главного фасада или условной оси.

Центральная симметрия в живописи

Центральная симметрия широко применяется и в изобразительном искусстве. С ее помощью художники создают гармоничные, статичные композиции. Например, на иконах часто изображают симметричные фигуры относительно центра или вертикальной оси.

Центрально-симметричные объекты в природе

Удивительно, но многие живые организмы тоже демонстрируют свойства центральной симметрии. Это можно объяснить тем, что такая симметричная форма является оптимальной и устойчивой в данных условиях существования.

Классические примеры - морские звезды, иглокожие, снежинки, цветы подсолнечника и ромашки. У них наблюдается правильное чередование элементов относительно центра.