Прямо пропорционально это как? Связанные величины при равномерном движении

Прямая пропорциональность является важной математической концепцией, которая описывает линейную зависимость между двумя переменными. Эта зависимость широко используется в науке, экономике и повседневной жизни для моделирования и анализа различных процессов.

Понятие прямой пропорциональности

Прямо пропорциональными называются две величины x и y, если их отношение y/x остается постоянным при любых значениях этих величин. Это постоянное отношение обозначают через k и называют коэффициентом пропорциональности :

y/x = k

Например, если стоимость 1 кг конфет составляет 40 рублей, то стоимость 3 кг этих же конфет будет равна 120 рублям. Здесь коэффициент пропорциональности k = 40 руб/кг показывает, что стоимость конфет линейно зависит от их количества.

Формула и график прямой пропорциональности

Формула прямой пропорциональной зависимости имеет вид:

y = kx

Где:

• x - независимая переменная
• y - зависимая переменная
• k - коэффициент пропорциональности

На координатной плоскости графиком прямой пропорциональности является прямая линия, проходящая через начало координат. Угол наклона этой прямой к оси абсцисс определяется коэффициентом пропорциональности k.

Примеры прямой пропорциональности

Прямая пропорциональность широко встречается в реальных процессах.

Физика. При равномерном движении пройденный путь прямо пропорционален времени. Чем больше времени движется тело, тем большее расстояние оно пройдет. Здесь скорость движения играет роль коэффициента пропорциональности.

Экономика. Стоимость товара прямо пропорциональна его количеству. Чем больше единиц товара приобретается, тем выше его общая цена. Цена за единицу товара - это коэффициент пропорциональности.

Бизнес. Выручка компании прямо пропорциональна объему продаж. Чем больше товаров или услуг реализуется, тем выше совокупная выручка. Коэффициентом пропорциональности здесь является цена реализации единицы продукции.

Свойства прямой пропорциональности

Прямо пропорциональные величины обладают two основными свойствами:

1. Их отношение постоянно и равно коэффициенту пропорциональности k.
2. Результат умножения пропорциональных величин также пропорционален каждой из них.

Эти свойства позволяют преобразовывать формулы и уравнения, содержащие прямо пропорциональные величины. Например, в формуле пути S = v * t скорость v и время t являются прямо пропорциональными величинами. Изменение любой из них приведет к пропорциональному изменению пройденного пути S.

Применение прямой пропорциональности

Понимание прямой пропорциональной зависимости важно для решения многих практических задач:

• Расчет времени и стоимости поездки транспорта
• Определение оптимального объема производства и цены товара
• Планирование бюджета рекламной кампании
• Прогнозирование прибыли в зависимости от цены и спроса

Во всех этих случаях используется модель линейной зависимости одной величины от другой. Поэтому умение распознавать и применять прямую пропорциональность крайне полезно в решении широкого круга задач.

Отличие от обратной пропорциональности

В отличие от прямой пропорциональности, при обратной пропорциональности увеличение одной величины ведет к уменьшению другой. Например, при постоянной скорости чем больше времени движется автомобиль, тем меньше остается до пункта назначения.

Здесь с увеличением времени в пути расстояние до пункта назначения уменьшается. Поэтому время и оставшееся расстояние являются обратно пропорциональными величинами.

Закономерности прямой пропорциональности

Хотя формула прямой пропорциональности довольно проста, эта зависимость подчиняется важным количественным закономерностям. Рассмотрим некоторые из них.

Масштабирование

Если одну из прямо пропорциональных величин увеличить или уменьшить в несколько раз, то во столько же раз изменится и другая величина. Например, если скорость движения вырастет в 2 раза, то за то же время будет пройден путь, больший тоже в 2 раза.

Сложение пропорциональных величин

Сумма двух пропорциональных величин пропорциональна каждой из них в отдельности. Так, если за первый час работы выполнено 10 единиц продукции, а за второй час - 15 единиц, то общее количество 25 единиц пропорционально длительности работы.

Деление пропорциональных величин

Частное от деления двух прямо пропорциональных величин есть величина постоянная, не зависящая от их значений. Например, отношение пути ко времени движения постоянно и равно скорости.

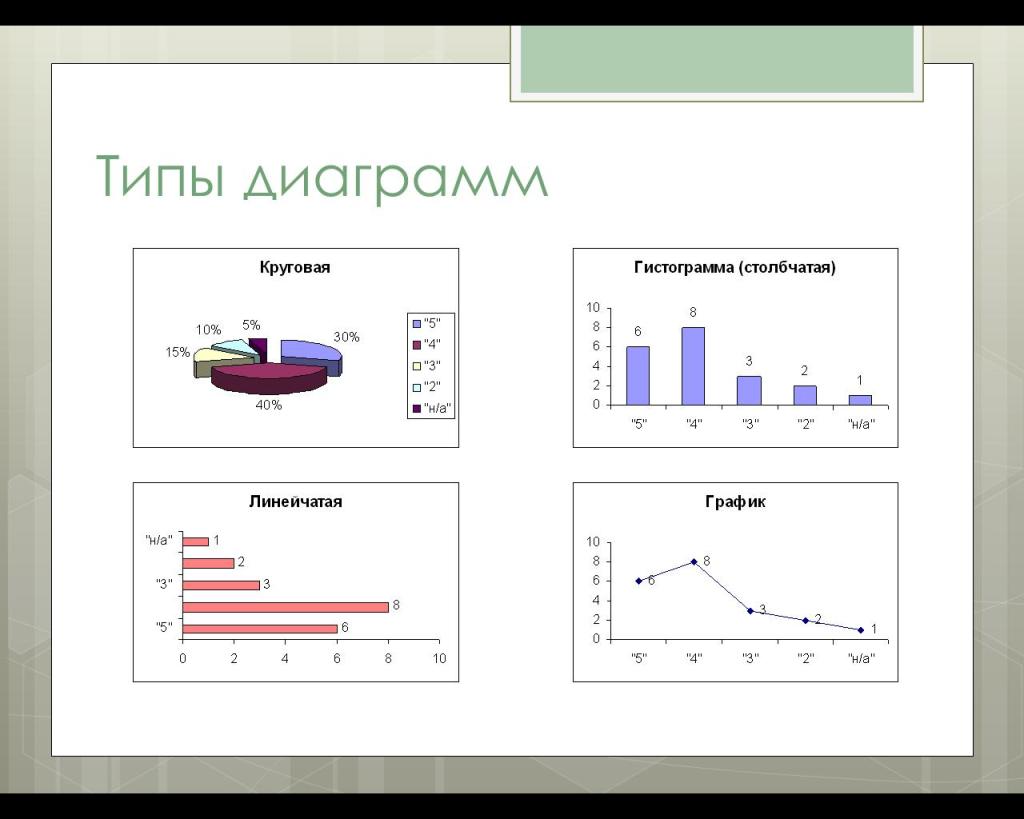
Графическое представление данных

Для наглядности зависимости между прямо пропорциональными величинами удобно использовать различные типы графиков и диаграмм:

• Линейный график
• Гистограмма
• Круговая диаграмма

Это позволяет быстро увидеть, каким образом изменение одной величины сказывается на другой. К примеру, зависимость выручки магазина от количества проданных товаров можно представить в виде линейного графика или столбчатой диаграммы.

Прямая пропорциональность в задачах

Чтобы грамотно решать текстовые задачи, содержащие прямо пропорциональные величины, нужно:

1. Выявить между какими величинами присутствует прямая пропорциональность
2. Определить коэффициент пропорциональности
3. Записать формулу зависимости
4. Найти искомую величину путем математических преобразований

К примеру, по известной стоимости 2 кг конфет надо найти цену 5 кг. Сначала определяем, что стоимость прямо пропорциональна массе. Затем находим коэффициент пропорциональности и подставляем значения в формулу прямой пропорциональности.

Решение задач на прямую пропорциональность

Рассмотрим подробный алгоритм решения задач, содержащих прямо пропорциональные величины:

Анализ условия задачи

На этом этапе нужно:

• Выделить, какие величины даны в условии задачи
• Определить, между какими величинами существует прямая пропорциональность

Выбор переменных

Обозначим буквами:

• Одну из исходных величин, значение которой известно
• Вторую исходную величину, если ее значение тоже дано
• Искомую величину через х

Запись пропорции

Составим пропорцию из отношения одноименных величин и коэффициента пропорциональности:

Известная величина 1 / Известная величина 2 = k Искомая величина / Известная величина 1 = k

Вычисление неизвестной величины

Находим значение искомой величины путем математических преобразований:

x = k * Известная величина 1

Проверка ответа

Подставляем найденное значение в исходную пропорцию и проверяем равенство отношений.