Признаки подобия треугольников и их практическое применение для решения задач

Понятие подобия произвольных геометрических фигур, в сущности, очень просто можно объяснить и тем более доказать. Так, например, разглядывая предмет через лупу, мы видим увеличенное в несколько раз изображение этого предмета с сохранением пропорций всех его размеров. Иными словами, изображение предмета аналогично исходному объекту до увеличения. В большинстве задач по геометрии для доказательства пропорциональности сторон и площадей треугольников применяются основные 3 признака. Для того чтобы рассмотреть существующие признаки подобия треугольников, необходимо изначально определиться с ключевым понятием, которое будет в дальнейшем использоваться в тексте.

Итак, треугольники являются подобными, если их аналогично расположенные стороны пропорциональны, а соответственно расположенные углы равны (стоит помнить о том, что стороны называются аналогичными, или соответствующими, если они расположены напротив одинаковых по величине углов). Рассмотрим подобные треугольники ∆АВС и ∆А₁B₁C₁. Согласно выше изложенному понятию, соответствующими сторонами являются: АВ и А₁B₁, а также пары сторон BC и B₁C₁, АС и А₁C₁. Обратите внимание, что стороны каждой из этих трёх пар лежат напротив одинаковых по величине углов.

Подобие обозначается специальным символом, который ставится между обозначениями рассматриваемых фигур: ∆АВС ∼ ∆ А₁B₁C₁.

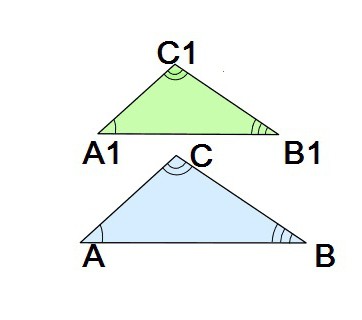
Отношение соответствующих сторон при при наличии данного признака - это параметр, называемый коэффициентом подобия k. В случае если k = 2, то можно сказать, что одна из двух рассматриваемых геометрических фигур является увеличенной в два раза копией другой. Ясно, что в случае если k = 1, то треугольники равны. Таким образом, данное равенство можно считать некоторым частным случаем их подобия.

Признаки подобия треугольников

Оказывается, для установления факта наличия рассматриваемого признака нет нужды проверять все требования, перечисленные в формулировке определения подобия, данного выше. Достаточно лишь выполнения минимального набора условий, и это мы сейчас подтвердим на практике.

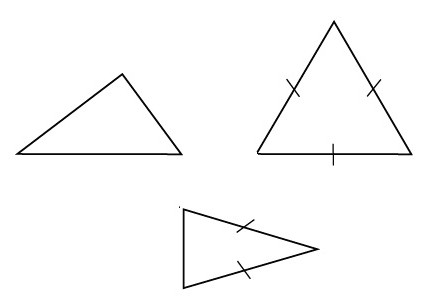
Первый признак

При решении задач первый признак подобия треугольников фигурирует в доказательствах намного чаще, чем остальные. Обратите внимание, что он оперирует всего двумя элементами геометрической фигуры: двумя углами. Остальные признаки подобия треугольников требуют для доказательства участия трех элементов. Итак, для двух произвольных подобных треугольников 2 угла одного из них равны аналогичным 2-м углам другого.

Доказательство

Согласно основным свойствам, действующим для любого произвольного треугольника, можно записать следующее выражение для ∠С. Его величина будет равна (180° - (∠А+∠В)), для другого ∠С₁ величина будет рассчитана по такому же принципу. Путем элементарных преобразований выражений получаем, что ∠С=∠С₁. Таким образом, все углы, имеющиеся в ∆АВС, равны всем аналогичным углам, расположенным в ∆А₁В₁С₁. По аналогичному алгоритму доказываются остальные признаки подобия треугольников.

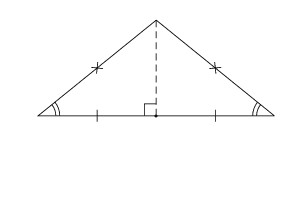
Второй признак

Этот подход к доказательству достаточно часто применяют, если известны углы рассматриваемых геометрических фигур.

Для двух подобных треугольников справедливо утверждение о том, что 2 стороны любого из них пропорциональны 2-м аналогичным сторонам другого, и при этом углы, расположенные между этими парами сторон, равны.

Доказательство

Для доказательства данного признака необходимо обратиться к предыдущим выкладкам. Исходя из приведенных выше результатов, нам достаточно доказать, что ∠В = ∠В₁. Рассмотрим ∆АВС₂, для которого, согласно первому признаку, справедливы следующие утверждения: ∠1=∠А₁, ∠2=∠В₁. ∆АВС₂~∆А₁В₁С₁. Значит, АВ/А₁В₁=АС₂/А₁С. С другой стороны, известно из условия, что имеет место соотношение вида: АС/А₁С₁₌АВ/А₁В₁. В результате получаем равенство сторон АС=АС₂, а также утверждение о том, что ∆АВС ~ ∆АВС₂ по второму признаку (АС=АС₂ и ∠А=∠1, так как в результате рассмотрения исходных данных установили, что А=∠А₁ и ∠1=∠А₁, АВ- является общей стороной для этих двух треугольников). Из доказательства следует, что ∠В=∠2, а так как ∠2=∠В₁, то получаем, что ∠В=∠В₁. Из чего следует, что еще один признак доказан.

Третий признак

Данный признак считается наиболее очевидным при доказательстве подобия, поскольку рассматриваются все стороны данных треугольников с известными параметрами.

Итак, для двух треугольников, которые подобны друг другу, имеет место утверждение о том, что 3 стороны одного из них пропорциональны 3-м соответствующим сторонам другого.

Доказательство

Учитывая предыдущий признак подобия, теперь для построения доказательства достаточно лишь установить то, что существует равенство вида: ∠A=∠A₁. Для этого рассмотрим любой произвольный ∆АВС₂, у которого ∠1=∠A₁, ∠2=∠В₁. По 1-му признаку ∆АВС₂ ∼ ∆А₁B₁C₁, следовательно для этих двух треугольников можем записать соотношение вида АВ/А₁В₁=ВС₂/В₁С₁ =С₂А/С₁А_1, из которого можно записать равенства вида: В₁С₁=ВС₂, А₁С₁=АС₂. Из этого логично заключить, что ∆АВС ∼ ∆АВС_2, и, как вывод, ∠А и ∠А₁ равны. Из чего следует, что рассматриваемый признак также доказан.

Свойства

1. Для двух треугольников, подобных друг другу, отношение величин их площадей прямо пропорционально коэффициенту, возведенному в квадрат. Доказательство. Рассмотрим две произвольных фигуры, имеющих по три стороны и три угла, которые подобны друг другу. Пусть А и А₁ — соответствующие стороны данных фигур, а h и h₁ — соответствующие высоты. Пусть k - коэффициент подобия для рассматриваемых треугольников, следовательно, из соотношения сторон можем записать уравнение вида: А₁= к*А. Нетрудно увидеть, что и для соотношения высот можем записать уравнение вида: h₁= к*h. Для отношения площадей рассматриваемых геометрических фигур получаем: S₁/S=(1/2a₁h₁) /(1/2ah)=(a₁/a)*(h₁/h)= k*k = k². Таким образом, при «растяжении» треугольника в 2 раза его площадь увеличивается в 2²= 4 раза. Второе свойство вытекает из предыдущего доказательства и напрямую с ним связано.
2. Все соответствующие линии, проведенные в подобных треугольниках, также пропорциональны между собой и равны величине выявленного выше коэффициента. То есть, согласно приведенному выше свойству, можно утверждать, что все внутренние дополнительные построения также будут пропорциональны.

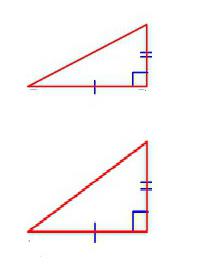
Дополнение к основному перечню признаков

Стоит рассмотреть еще ряд отдельных признаков, которые применимы для геометрических фигур определенного вида. Итак, прямоугольные треугольники являются подобными, если:

• их гипотенузы и любой из двух катетов соответственно пропорциональны;
• если их соответствующие острые углы равны;
• если все катеты рассматриваемых треугольников попарно пропорциональны.

Заключение

Таким образом, мы объединили все возможные признаки, с помощью которых можно так или иначе доказать подобие двух и более фигур с тремя углами и сторонами, независимо от их вида и свойств. В большинстве задач по геометрии для доказательства пропорциональности сторон и площадей применяются основные три признака, но мы не оставили без внимания ряд признаков подобия, которые применимы лишь в случае, если необходимо осуществить доказательство для рассматриваемых геометрических фигур с наличием прямого угла. Данные признаки подобия прямоугольных треугольников значительно упрощают процесс решения различного рода задач и требуют для них минимум данных.