Прямоугольный треугольник и его свойства

Прямоугольный треугольник – треугольник, один угол которого прямой (равен 90⁰). Следовательно, два других угла в сумме дают 90⁰.

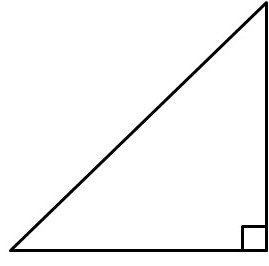
Стороны прямоугольного треугольника

Сторона, которая располагается напротив угла в девяносто градусов, называется гипотенузой. Две другие стороны именуются катетами. Гипотенуза всегда длиннее, чем катеты, но короче их суммы.

Прямоугольный треугольник. Свойства треугольника

Если катет находится напротив угла в тридцать градусов, то его длина соответствует половине длины гипотенузы. Отсюда вытекает, что угол, противоположный катету, длина которого соответствует половине гипотенузы, равен тридцати градусам. Катет равняется среднему пропорциональному гипотенузы и проекции, которую дает катет на гипотенузу.

Теорема Пифагора

Любой прямоугольный треугольник подчиняется теореме Пифагора. Эта теорема гласит, что сумма квадратов катетов равна квадрату гипотенузы. Если принять, что катеты равны а и в, а гипотенуза – с, то запишем: а²+в²=с². Теорема Пифагора применяется для решения всех геометрических задач, в которых фигурируют прямоугольные треугольники. Также она поможет начертить прямой угол при отсутствии необходимых инструментов. 

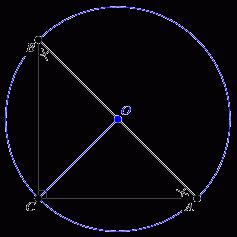
Высота и медиана

Прямоугольный треугольник характеризуется тем, что две его высоты совмещаются с катетами. Чтобы найти третью сторону, нужно найти сумму проекций катетов на гипотенузу и разделить на два. Если из вершины прямого угла провести медиану, то она окажется радиусом окружности, которую описали вокруг треугольника. Центром этой окружности будет середина гипотенузы.

Прямоугольный треугольник. Площадь и ее вычисление

Площадь прямоугольных треугольников вычисляется по любой формуле нахождения площади треугольника. Помимо этого, можно использовать еще одну формулу: S=а*в/2, которая гласит, что для нахождения площади нужно произведение длин катетов разделить на два.

Косинус, синус и тангенс прямоугольного треугольника

Косинусом острого угла именуют отношение катета, прилегающего к углу, к гипотенузе. Он всегда меньше, чем единица. Синус – это отношение катета, который лежит напротив угла, к гипотенузе. Тангенс – отношение катета, лежащего против угла, к катету, прилегающему к этому углу. Котангенсом называют отношение катета, прилегающего к углу, к катету, находящемуся напротив угла. Косинус, синус, тангенс и котангенс не являются зависимыми от размеров треугольника. На их значение влияет только градусная мера угла.

Решение треугольника

Чтобы вычислить значение катета, противолежащего углу, нужно умножить длину гипотенузы на синус этого угла или размер второго катета на тангенс угла. Для нахождения катета, прилежащего к углу, необходимо посчитать произведение гипотенузы на косинус угла.

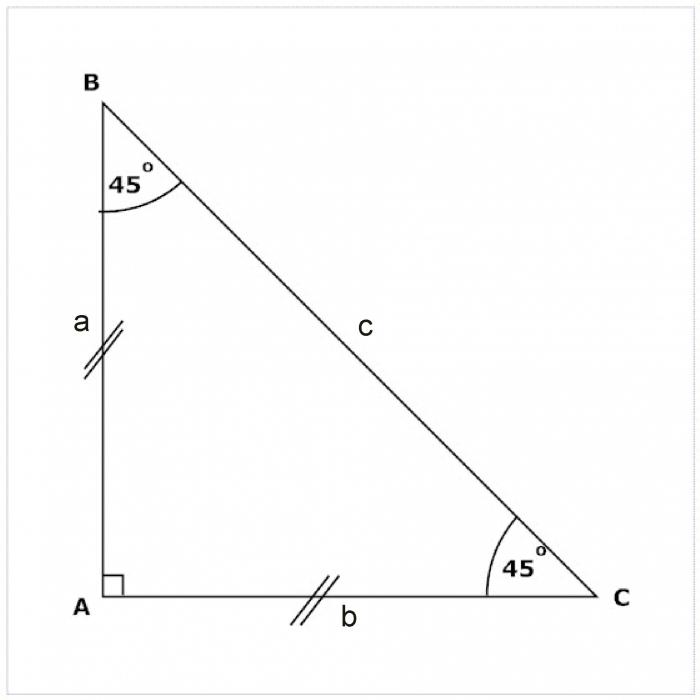
Равнобедренный прямоугольный треугольник

Если треугольник имеет прямой угол и равные катеты, то его называют равнобедренным прямоугольным треугольником. Острые углы такого треугольника тоже равны - по 45⁰. Медиана, биссектриса и высота, проведенные из прямого угла равнобедренного прямоугольного треугольника, совпадают.