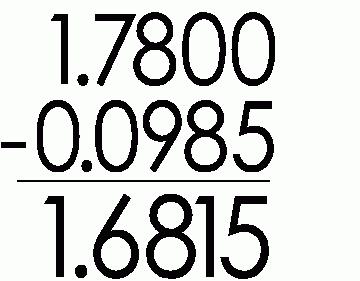Десятичные дроби и действия с ними. Деление и умножение десятичных дробей

Десятичная дробь используется, когда нужно выполнять действия с нецелыми числами. Это может показаться нерациональным. Но такой вид чисел существенно облегчает математические операции, которые с ними необходимо выполнять. Это понимание приходит со временем, когда их запись становится привычной, а прочтение не вызывает трудностей, и освоены правила десятичных дробей. Тем более что все действия повторяют уже известные, которые усвоены с натуральными числами. Только нужно запомнить некоторые особенности.

Определение десятичной дроби

Десятичная дробь — это особое представление нецелого числа со знаменателем, который делится на 10, а ответ получается в виде единицы и, возможно, нулей. Другими словами, если в знаменателе 10, 100, 1000 и так далее, то удобнее переписать число с использованием запятой. Тогда до нее будет расположена целая часть, а потом - дробная. Причем запись второй половины числа будет зависеть от знаменателя. Количество цифр, которые находятся в дробной части, должно быть равно разряду знаменателя.

Проиллюстрировать вышесказанное можно этими числами:

9/10=0,9; 178/10000=0,0178; 3,05; 56 003,7006.

Причины, по которым понадобилось применение десятичных дробей

Математикам потребовались десятичные дроби по нескольким основаниям:

1. Упрощение записи. Такая дробь расположена вдоль одной линии без черточки между знаменателем и числителем, при этом наглядность не страдает.

2. Простота в сравнении. Достаточно просто соотнести цифры, находящиеся в одинаковых позициях, в то время как с обыкновенными дробями пришлось бы приводить их к общему знаменателю.

3. Упрощение вычислений.

4. Калькуляторы не рассчитаны на введение обыкновенных дробей, они для всех операций используют десятичную запись чисел.

Как правильно прочитать такие числа?

Ответ прост: так же, как обыкновенное смешанное число со знаменателем, кратным 10. Исключение составляют только дроби без целого значения, тогда при чтении нужно произносить «ноль целых».

Например, 45/1000 нужно произнести как сорок пять тысячных, в то же время 0,045 будет звучать как ноль целых сорок пять тысячных.

Смешанное число с целой частью равной 7 и дробью 17/100, что запишется как 7,17, в обоих случаях будет прочитано как семь целых семнадцать сотых.

Роль разрядов в записи дробей

Верно отметить разряд - это то, что требует математика. Десятичные дроби и их значение могут существенно измениться, если записать цифру не в том месте. Впрочем, это было справедливо и раньше.

Для прочтения разрядов целой части десятичной дроби нужно просто воспользоваться правилами, известными для натуральных чисел. А в правой части они зеркально отражаются и по-другому читаются. Если в целой части звучало "десятки", то после запятой это будут уже "десятые".

Наглядно это можно увидеть в этой таблице.

Как правильно записать смешанное число десятичной дробью?

Если в знаменателе стоит число, равное 10 или 100, и прочие, то вопрос о том, как дробь перевести в десятичную, несложен. Для этого достаточно по-другому переписать все ее составные части. В этом помогут такие пункты:

• немного в стороне написать числитель дроби, в этот момент десятичная запятая располагается справа, после последней цифры;

• переместить запятую влево, здесь самое главное - правильно сосчитать цифры — передвинуть ее нужно на столько позиций, сколько нолей в знаменателе;

• если их не хватает, то на пустых позициях должны оказаться нули;

• нули, которые были в конце числителя, теперь не нужны, и их можно зачеркнуть;

• перед запятой приписать целую часть, если ее не было, то здесь тоже окажется нуль.

Внимание. Нельзя зачеркивать нули, которые оказались окружены другими цифрами.

О том, как быть в ситуации, когда в знаменателе число не только из единицы и нулей, как дробь переводить в десятичную, можно прочитать чуть ниже. Это важная информация, с которой обязательно стоит ознакомиться.

Как дробь перевести в десятичную, если знаменатель - произвольное число?

Здесь возможны два варианта:

1. Когда знаменатель можно представить в виде числа, которое равно десяти в любой степени.

2. Если такую операцию проделать нельзя.

Как это проверить? Нужно разложить знаменатель на множители. Если в произведении присутствуют только 2 и 5, то все хорошо, и дробь легко преобразуется в конечную десятичную. В противном случае, если появляются 3, 7 и другие простые числа, то результат будет бесконечным. Такую десятичную дробь для удобства использования в математических операциях принято округлять. Об этом будет речь немного ниже.

Изучает, как получаются такие десятичные дроби, 5 класс. Примеры здесь будут очень кстати.

Пусть в знаменателях находятся числа: 40, 24 и 75. Разложение на простые множители для них будет такое:

• 40=2·2·2·5;
• 24=2·2·2·3;
• 75=5·5·3.

В этих примерах только первая дробь может быть представлена в виде конечной.

Алгоритм перевода обыкновенной дроби в конечную десятичную

• Проверить разложение знаменателя на простые множители и убедиться в том, что оно будет состоять из 2 и 5.

• Добавить к этим числам столько 2 и 5, чтобы их стало равное количество. Они дадут значение дополнительного множителя.

• Произвести умножение знаменателя и числителя на это число. В результате получится обыкновенная дробь, под чертой у которой стоит 10 в некоторой степени.

• Дальше действовать так, как было описано в пункте, расположенном немного выше.

Если в задаче эти действия выполняются со смешанным числом, то его сначала нужно представить в виде неправильной дроби. А уже потом действовать по описанному сценарию.

Представление обыкновенной дроби в виде округленной десятичной

Этот способ того, как дробь переводить в десятичную, кому-то покажется даже проще. Потому что в нем нет большого количества действий. Нужно только разделить значение числителя на знаменатель.

К любому числу с десятичной частью справа от запятой можно приписать бесконечное количество нулей. Этим свойством и нужно воспользоваться.

Сначала записать целую часть и поставить после нее запятую. Если дробь правильная, то написать ноль.

Потом полагается выполнить деление числителя на знаменатель. Так, чтобы количество цифр у них было одинаковым. То есть приписать справа у числителя нужное количество нолей.

Выполнять деление в столбик до тех пор, пока не будет набрано нужное количество цифр. Например, если округлить нужно будет до сотых, то в ответе их должно быть 3. В общем, цифр должно быть на одну больше, чем нужно получить в итоге.

Записать промежуточный ответ после запятой и округлить по правилам. Если последняя цифра - от 0 до 4, то ее нужно просто отбросить. А когда она равна 5-9, то стоящую перед ней нужно увеличить на единицу, отбросив последнюю.

Возврат от десятичной дроби к обыкновенной

В математике встречаются задачи, когда десятичные дроби удобнее представить в виде обыкновенных, в которых есть числитель со знаменателем. Можно вздохнуть с облегчением: эта операция возможна всегда.

Для этой процедуры нужно сделать следующее:

• записать целую часть, если она равна нулю, то ничего писать не надо;

• провести дробную черту;

• над ней записать цифры из правой части, если первыми идут нули, то их нужно зачеркнуть;

• под чертой написать единицу с таким количеством нолей, сколько цифр стоит после запятой в первоначальной дроби.

Это все, что нужно сделать, чтобы перевести десятичную дробь в обыкновенную.

Что можно делать с десятичными дробями?

В математике это будут определенные действия с десятичными дробями, которые ранее выполнялись для других чисел.

Ими являются:

• сравнение;

• сложение и вычитание;

• умножение и деление.

Первое действие, сравнение, похоже на то, как это делалось для натуральных чисел. Чтобы определить, какое больше, нужно сравнивать разряды целой части. Если они окажутся равными, то переходят к дробной и так же по разрядам сравнивают их. То число, где окажется большая цифра в старшем разряде, и будет ответом.

Сложение и вычитание десятичных дробей

Это, пожалуй, самые простые действия. Потому что выполняются по правилам для натуральных чисел.

Так, чтобы выполнить сложение десятичных дробей, их нужно записать друг под другом, разместив запятые в столбик. При такой записи слева от запятых оказываются целые части, а справа — дробные. И теперь нужно сложить цифры поразрядно, как это делается с натуральными числами, снеся вниз запятую. Начинать сложение нужно с самого маленького разряда дробной части числа. Если в правой половине не хватает цифр, то дописывают нули.

При вычитании действуют так же. И здесь действует правило, которое описывает возможность занять единицу у старшего разряда. Если в уменьшаемой дроби после запятой меньше цифр, чем у вычитаемого, то в ней просто приписывают нули.

Немного сложнее обстоит дело с заданиями, где нужно выполнить умножение и деление десятичных дробей.

Как умножить десятичную дробь в разных примерах?

Правило, по которому производится умножение десятичных дробей на натуральное число, такое:

• записать их в столбик, не обращая внимания на запятую;

• перемножить, как если бы они были натуральными;

• отделить запятой столько цифр, сколько их было в дробной части исходного числа.

Частным случаем является пример, в котором натуральное число равно 10 в любой степени. Тогда для получения ответа нужно просто передвинуть запятую вправо на столько позиций, сколько нулей в другом множителе. Иными словами, при умножении на 10 запятая сдвигается на одну цифру, на 100 - их будет уже две, и так далее. Если цифр в дробной части не хватает, то нужно записать на пустых позициях нули.

Правило, которым пользуются, когда в задании нужно произвести умножение десятичных дробей на другое такое же число:

• записать их друг под другом, не обращая внимания на запятые;

• умножить, как если бы они были натуральными;

• отделить запятой столько цифр, сколько их было в дробных частях обеих исходных дробях вместе.

Частным случаем выделяются примеры, в которых один из множителей равен 0,1 или 0,01 и далее. В них нужно выполнить перемещение запятой влево на количество цифр в представленных множителях. То есть если умножается на 0,1, то запятая сдвигается на одну позицию.

Как разделить десятичную дробь в разных заданиях?

Деление десятичных дробей на натуральное число выполняется по такому правилу:

• записать их для деления в столбик, как если бы они были натуральными;

• делить по привычному правилу до тех пор, пока не закончится целая часть;

• поставить в ответ запятую;

• продолжить деление дробной составляющей до получения в остатке нуля;

• если нужно, то можно приписать нужное количество нулей.

Если целая часть равна нулю, то и в ответе ее тоже не будет.

Отдельно стоит деление на числа, равные десятке, сотне и так далее. В таких задачах нужно передвинуть запятую влево на количество нулей в делителе. Бывает, что цифр в целой части не хватает, тогда вместо них используют нули. Можно заметить, что эта операция подобна умножению на 0,1 и подобным ей числам.

Чтобы выполнить деление десятичных дробей, нужно воспользоваться этим правилом:

• превратить делитель в натуральное число, а для этого перенести в нем запятую вправо до конца;

• выполнить перемещение запятой и в делимом на такое же число цифр;

• действовать по предыдущему сценарию.

Выделяется деление на 0,1; 0,01 и прочие подобные числа. В таких примерах запятая сдвигается вправо на число цифр в дробной части. Если они закончились, то нужно приписать недостающее количество нулей. Стоит отметить, что это действие повторяет деление на 10 и подобные ему числа.

Заключение: все дело в практике

Ничто в учебе не дается легко и без усилий. Для надежного освоения нового материала требуются время и тренировка. Математика не исключение.

Чтобы тема про десятичные дроби не вызывала затруднений, нужно решать с ними примеров как можно больше. Ведь было время, когда и сложение натуральных чисел ставило в тупик. А теперь все нормально.

Поэтому, перефразируя известную фразу: решать, решать и еще раз решать. Тогда и задания с такими числами будут выполняться легко и непринужденно, как очередная головоломка.

Кстати, и головоломки поначалу решаются сложно, а потом нужно делать привычные движения. Так же и в математических примерах: пройдя по одному пути несколько раз, потом уже не будешь задумываться над тем, куда повернуть.