Абсолютно упругий удар. Абсолютно неупругий удар

Законы сохранения импульса – фундаментальные законы природы. Примером применения этих законов может быть явление соударения. Абсолютно упругий и неупругий удары – изменение состояния тел в результате кратковременного взаимодействия при их столкновении.

Механизм взаимодействия

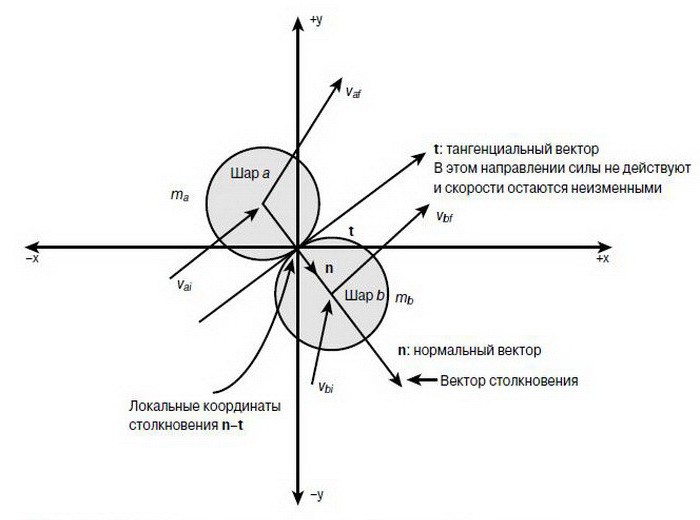
Простейшим видом взаимодействий физических тел является центральное столкновение шаров, имеющих идеальную геометрическую форму. Время контакта этих объектов укладывается в сотые доли секунды.

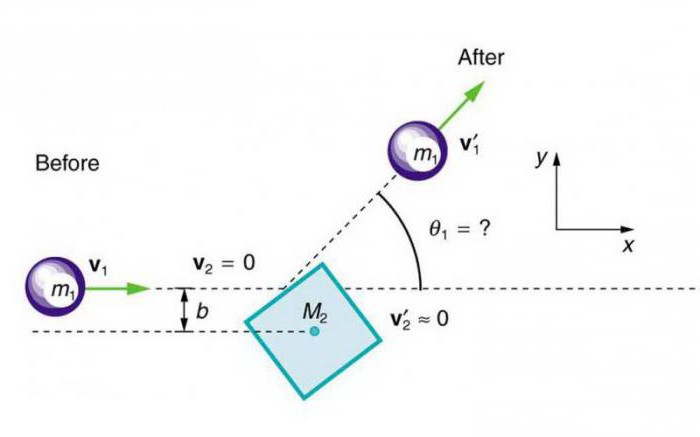
Согласно определению, центральным считается удар, при котором линия столкновения пересекает центры шаров. При этом траектория взаимодействия – это прямая, проведенная точно к элементу поверхности соприкосновения в момент контакта. В механике различают абсолютно упругий и неупругий удары.

Типы взаимодействий

Абсолютно неупругий удар наблюдается при столкновении двух тел из пластичных материалов или пластичного и упругого тел. После его совершения скорости соударяющихся объектов становятся одинаковыми.

Абсолютно упругий удар наблюдается при взаимодействии объектов, изготовленных из упругих материалов (например, двух шариков из твердых сортов стали либо шариков из некоторых видов пластмасс и т. д.).

Этапы

Процесс упругого соударения происходит в два этапа:

• I этап – момент после начала столкновения. Силы, действующие на шарики, увеличиваются с ростом деформации. Увеличение деформации сопровождается изменением скорости объектов. Тела, скорость которых была больше, замедляют свое движение, а тела с меньшей скоростью ускоряются. Когда деформация станет максимальной, скорость шаров после абсолютно упругого удара становится равновесной.
• II этап. С момента, который характеризует начало второго этапа упругого удара, значение деформаций уменьшается. При этом силы деформации расталкивают шарики. После исчезновения деформации, шарики удаляются и полностью восстанавливают свою первоначальную форму и движутся с разными скоростями. Таким образом, в конце второго этапа центральный абсолютно упругий удар превращает весь запас потенциальной энергии упругодеформированных тел в кинетическую энергию.

Изолированные системы

На практике ни один удар не является абсолютным (упругим либо неупругим). Система в любом случае взаимодействует с окружающим веществом, обменивается энергией и информацией со средой. Но для теоретических исследований допускается существование изолированных систем, в которых взаимодействуют исключительно объекты исследований. Например, возможен как абсолютно неупругий, так и абсолютно упругий удар шаров.

Внешние силы на такую систему не действуют либо их влияние скомпенсировано. В изолированной системе закон сохранения импульсов работает в полной мере – полный импульс между сталкивающимися телами сохраняется:

∑=m_iv_i=const.

Здесь «m» и «v» – масса некой частицы («i») изолированной системы и вектор ее скорости соответственно.

Для сохранения механической энергии (частного случая общего закона энергий) есть необходимость, чтобы силы, которые действуют в системе, были консервативными (потенциальными).

Консервативные силы

Консервативными называются силы, которые не превращают в прочие виды энергий механическую энергию. Эти силы всегда потенциальны – то есть работа, которую выполняют такие силы по замкнутому контуру, равна нулю. В противном случае силы называются диссипативными или неконсервативными.

В консервативных изолированных системах механическая энергия между сталкивающимися телами также сохраняется:

W=Wk+Wp=∑(mv²/2)+Wp=const.

Здесь Wk и Wp – кинетическая (k) и потенциальная (p) энергии соответственно.

Для проверки актуальности законов сохранения энергий (приведенных выше формул), если совершаются удары абсолютно упругих тел при условии, что до столкновения один из шаров не двигается (скорость неподвижного тела v₂=0), ученые вывели следующую закономерность:

m₁v₁Ki=m₁U₁+m₂U₂

(m₁v₁²)/2×Ke=(m₁U₁²)/2+(m₂U₂²)/2.

Здесь m₁ и m₂ – масса первого (ударного) и второго (неподвижного) шаров. Ki и Ke – коэффициенты, показывающие, во сколько раз увеличился импульс двух шаров (Ki) и энергия (Ke) в момент, когда совершается абсолютно упругий удар. v₁ – скорость подвижного шара.

Поскольку суммарный импульс системы должен сохраняться при любых условиях столкновений, то следует ожидать, что коэффициент восстановления импульса будет равен единице.

Расчет силы удара

Скорость ударного (отклоняемого на нити) шара, которая налетает на неподвижный (свободно подвешенный на нити) шар, определяется формулой закона сохранения энергии:

m₁gh=(m₁v₁²)/2

h=l-lcosα=2lsin²(α/2).

Здесь h – величина отклонения плоскости ударного шара относительно плоскости неподвижного шара. l – длина нитей (абсолютно одинаковы), на которых подвешены шары. α – угол отклонения ударного шара.

Соответственно, абсолютно упругий удар при столкновении ударного (отклоняемого на нити) и неподвижного (свободно висящего на нити) шара рассчитывается по формуле:

v₁=2sin(α/2)√gl.

Установка для исследований

На практике для расчета сил взаимодействия применяют простую установку. Она предназначена для изучения видов ударов двух шаров. Установка представляет собой треножник на трех винтах, которые позволяют выставить его по горизонтали. На треножнике расположена центральная стойка, к верхнему концу которой прикрепляют специальные подвесы для шаров. На штанге закреплен электромагнит, притягивающий и удерживающий в начале эксперимента в отклоненном состоянии один из шаров (ударный шар).

Величину начального угла отклонения этого шара (коэффициент α) можно определить по расходящейся в обе стороны дугообразной шкале. Величина ее искривления соответствует траектории перемещения взаимодействующих шаров.

Процесс исследования

Вначале подготавливается пара шаров: в зависимости от заданий берутся упругие, неупругие либо два разноплановых шара. В специальную таблицу записываются массы шаров.

Затем к электромагниту пристыковывается ударный элемент. По шкале определяют угол отклонения нити. Затем электромагнит отключают, он теряет притягивающие свойства, и шар по дуге устремляется вниз, сталкиваясь со вторым, свободным, неподвижно висящим шаром, который в результате импульса (удара) отклоняется на определенный угол. Величину отклонения фиксируют по второй шкале.

Абсолютно упругий удар рассчитывается на основании данных эксперимента. Для подтверждения правдивости законов сохранения импульса и энергии при упругом и неупругом ударах двух шаров определяют их скорости до и после столкновения. В основу положен баллистический метод измерения скорости движения шаров по величине их отклонения. Эта величина отсчитывается по шкалам, изготовленным в виде дуг окружности.

Особенности расчетов

При расчетах удара в классической механике не учитывают ряд показателей:

• время соударения;
• степень деформации взаимодействующих объектов;
• неоднородность материалов;
• скорость деформации (передачи импульса, энергии) внутри шара.

Столкновение бильярдных шаров – показательный пример упругого удара.