Ускорение свободного падения: открытие, причины, формула

Ускорение свободного падения – одно из множества открытий великого Ньютона, который не только суммировал опыт предшественников, но и дал строгое математическое объяснение огромному количеству фактов и экспериментальных данных.

Предпосылки открытия. Эксперименты Галилея

Один из многочисленных экспериментов Галилео Галилея был посвящен исследованию движения тел в полете. До этого в системе мировоззрения господствовало мнение, что более легкие тела падают медленнее, чем тяжелые. Бросая различные предметы с высоты Пизанской башни, Галилей установил, что ускорение свободного падения для тел с различной массой абсолютно одинаково.

Небольшие расхождения теории с экспериментальными данными Галилей справедливо отнес к влиянию сопротивления воздуха. Для доказательства своих рассуждений он предлагал повторить эксперимент в вакууме, но на тот момент техническая возможность для этого отсутствовала. Лишь через многие годы мысленный эксперимент Галилея провел Исаак Ньютон.

Теория Ньютона

Честь открытия закона всемирного тяготения принадлежит Ньютону, но сама идея уже около 200 лет витала в воздухе. Основной предпосылкой для формирования новых принципов небесной механики стали законы Кеплера, сформулированные им на основе многолетних наблюдений. Из океана допущений и домыслов Ньютон извлек предположение о силе притяжения Солнца и расширил свою теорию до понятия о всемирном тяготении. Он проверил свою гипотезу об обратной пропорциональности силы квадрату расстояния, рассмотрев орбиту Луны. Последующие проверки этой идеи осуществлялись при помощи исследования движения спутников Юпитера. Результаты наблюдений показали, что между спутниками планет и самими планетами действуют те же силы, что и при взаимодействии Солнца и планет.

Открытие гравитационной составляющей

Сила притяжения Земли к Солнцу подчинялась формуле:

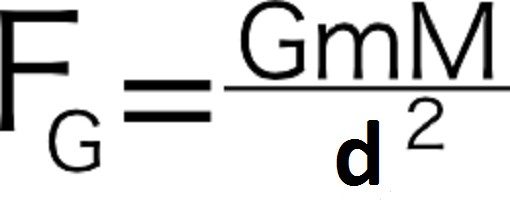
Эксперименты показали, что множитель 1/d² в этом соотношении был вполне применим и в случае рассмотрения других планет в Солнечной системе. Постоянная G являлась коэффициентом, приводившим значение пропорции к числовой величине.

Руководствуясь собственной теорией, Ньютон измерил соотношения масс различных небесных тел, например масса Юпитера / масса Солнца, масса Луны / масса Земли, но численный ответ на вопрос о том, сколько весит Земля, Ньютон дать не мог, так как постоянная G по-прежнему оставалась неизвестной.

Величина гравитационной постоянной была открыта лишь спустя полвека после смерти Ньютона. Оценки этой величины на основе гипотез, подобных предположениям Ньютона, показали, что данная величина является ничтожно малой, и в земных условиях вычислить ее значение практически невозможно. Обычная сила тяжести кажется огромной, поскольку все знакомые нам предметы невообразимо малы по сравнению с массой земного шара.

Конец 18 века. Измерение G

Первые попытки измерить G состоялись в конце 18 века. В качестве притягивающей силы они использовали гору огромных размеров. Оценка величины ускорения свободного падения производилась на основании отклонения от вертикали грузика маятника, расположенного в непосредственной близости от горы. С помощью геологических данных была произведена оценка массы горы и ее среднее расстояние от маятника. Так получили первое, довольно грубое измерение загадочной константы.

Измерения лорда Кавендиша

Лорд Кавендиш в своей лаборатории провел измерения гравитационного притяжения методом свободного взвешивания.

Для опытов был использован металлический шар и массивный кусок металла. Кавендиш прикреплял маленькие металлические шарики к тонкой планке и подносил к ним большие свинцовые шары. В результате воздействия планка закручивалась, пока эффект притяжения не компенсировал силы Гука. Эксперимент был настолько тонким, что даже малейшее дуновение ветерка могло свести на нет результаты исследований. Чтобы избежать конвекции, Кавендиш все измерительное оборудование разместил в большом коробе, затем поставил его в закрытой комнате, а наблюдения за экспериментом велись при помощи телескопа.

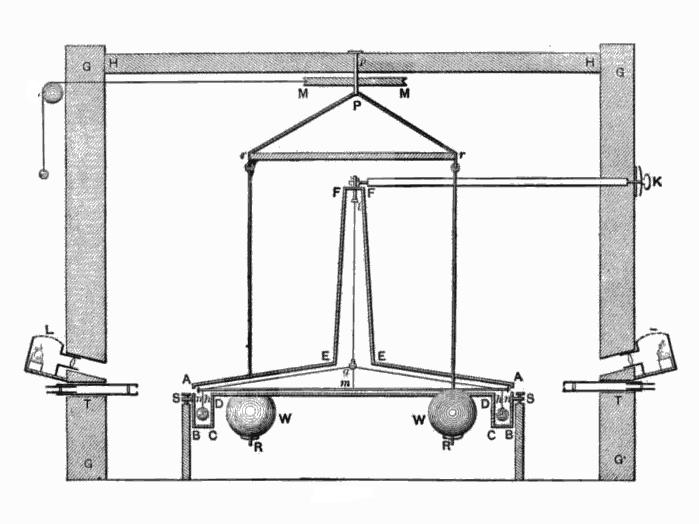
Вычислив силы закручивания нити, Кавендиш произвел оценку величины G, которая впоследствии была лишь немного откорректирована благодаря другим, более точным экспериментам. В современной системе единиц:

G =6.67384 × 10^-11 м³ кг^-1 с^-2.

Данная величина является одной из немногочисленных физических констант. Ее значение неизменно в любой точке Вселенной.

Измерение ускорения Земли

Согласно третьему закону Ньютона сила притяжения двух тел зависит лишь от их массы и расстояния между ними. Таким образом, подставляя в правую часть уравнения множитель, известный из второго закона Ньютона, получаем:

ma= G(mM)/d².

В нашем случае массу m можно сократить, а величина а и есть ускорение, с которым тело m притягивается к Земле. В настоящее время ускорение свободного падения принято обозначать буквой g. Получаем:

g = GM/d².

В нашем случае d –радиус Земли, М – ее масса, а G –та самая неуловимая константа, которую на протяжении многих лет искали физики. Подставляя в уравнение известные данные, получим: g=9,8м/с². Эта величина и составляет ускорение свободного падения на Земле.

Значения G для разных широт

Поскольку наша планета не имеет форму шара, а является геоидом, радиус ее не везде одинаков. Земля как бы сплюснута, поэтому на экваторе и на обоих полюсах ускорение свободного падения будет принимать различные значения. В целом разница в показаниях длины радиуса составляет около 43 км. Поэтому в физике для решения задач принимается то ускорение свободного падения, которое измерено на широте около 45⁰ . Довольно часто для облегчения расчетов его принимают равным 10 м/с².

Значение G для Луны

Наш спутник подчиняется тем же законам, что и остальные планеты Солнечной системы. Строго говоря, вычисляя ускорение на поверхности Луны, следует принимать во внимание и притяжение со стороны Солнца.

Но, как видно из формулы, с увеличением расстояния значение силы притяжения резко уменьшается. Поэтому, отбросив все второстепенные силы, используем ту же формулу:

G_Л = GM/d².

Здесь М – масса Луны, а d – ее диаметр. Подставив известные величины, получим величину G_Л=1,622 м/с². Эта величина и представляет собой ускорение свободного падения на Луне.

Именно такое малое значение G_Л является главной причиной того, что на Луне отсутствует атмосфера. По некоторым данным на заре времен наш спутник имел атмосферу, но из-за слабого притяжения Луна довольно быстро ее растеряла. Все планеты с большой массой обычно обладают собственной атмосферой. Ускорение свободного падения у них достаточно велико для того, чтобы не только не терять собственную атмосферу, но и прихватывать из космоса некоторое количество молекулярного газа.

Подведем некоторые итоги. Ускорение свободного падения - это величина, которой обладает каждое материальное тело. Как ни удивительно это звучит, но все, что обладает массой, притягивает к себе окружающие предметы. Просто это притяжение настолько мало, что в обычной жизни не играет никакой роли. Тем не менее ученые серьезно относятся даже к самым маленьким физическим константам, ведь влияние, которое они оказывают на окружающий мир, до конца еще нами не изучено.