Понятие матрицы и основные определения

Такое понятие, как матрица, используется и возникает в разделах высшей математики. Чаще всего она встречается в системе линейных уравнений. Так какое же основное понятие матрицы? Чтобы понять это, не обязательно быть математическим гением.

Матрица – это нечто такое, что представляет из себя систему из чисел mn, которые в математике записываются в виде таблиц, в которых m - это строки, а n – столбцы. На ее пересечении находятся элементы. Размер матрицы зависит от количества строк и столбцов.

Изначально рассматривалась матрица треугольной формы, но она не удобна для решения сложных уравнений, поэтому в математике используют прямоугольный аналог. Такая система считается удобной для решения поставленной задачи.

Откуда пришла матрица

Если говорить о первом упоминании, то понятие о матрице пришло из Китая, а точнее оно было связано с «магическими квадратами». Эти таблицы считались оберегами за счет начертанных на них чисел. В то время не было ни самого понятия матрицы, ни способов ее решения. Она определяла в некоторых племенах степень родства для того, чтобы люди узнавали, могут они пожениться или нет.

А вот само понятие было введено в начале 19 века Джеймсом Сильвестром, который был английским математиком. Над теорией матриц трудились различные ученые, создавая комплекс решений трудных алгебраических задач.

Матрица и ее основные виды

Итак, ранее было рассмотрено понятие матрицы. Виды матриц представлены ниже:

• Строчная. Она состоит из одной строки, то есть у этого вида матрицы количество строк ровно m=1, а вот количество ее столбцов произвольное.
• Столбцовая. Эта разновидность состоит всего из одного столбца, но также может содержать в себе нескольких строк. Для такого вида матрицы есть своя универсальная запись. Она указывает на то, что элементы, которые находятся в скобках, должны быть записаны в виде столбца. Ко всему прочему, это экономит не только место, но и время.
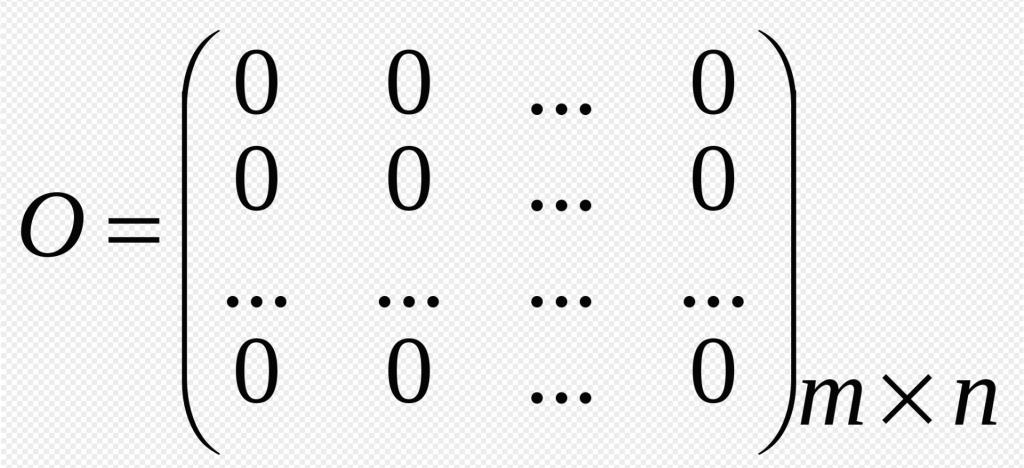
• Нуль-матрица. Такой вид существует, когда все ее элементы равны 0. Обозначают эту разновидность матрицы "О" Свое название этот элемент также получил за счет того, что в исчислении у нее схожие функции с нулем в теории чисел.
• Квадратная. Этот вид матрицы является самым распространенным, его отличие заключается в том, что в ней равное количество столбцов и строк. При соединении двух элементов, находящихся в разных концах столбца, мы получаем главную диагональ. В связи с этим диагональная таблица делится еще на несколько систем:

а) Диагональная. Этот тип квадратной матрицы, в которую не вошли элементы, принадлежащие главной диагонали.

б) Единичная. У такого типа диагональ состоит всего из одной единицы. При всем этом каждая такая матрица является скалярной.

в) Скалярная. Это тип, где главная диагональ состоит из одного и того же числа.

г) Стрелочная. Это вид квадратной матрицы, в которой практически все элементы равны нулю, но при этом составляющие, входящие в состав первого столбца, а также относящие к диагонали и первой строке, не равны ему.

• Бинарная. Этот вид таблицы состоит из нулей и единиц.
• Матрица Паскаля - в этом виде матрицы все элементы состоят из чисел, принадлежащих к одноименному треугольнику.
• Трехдиагональная. В этом виде матрицы ненулевые элементы расположены на трех диагоналях, к которым относится главная из них и те, что сверху и снизу.

Ранг матрицы

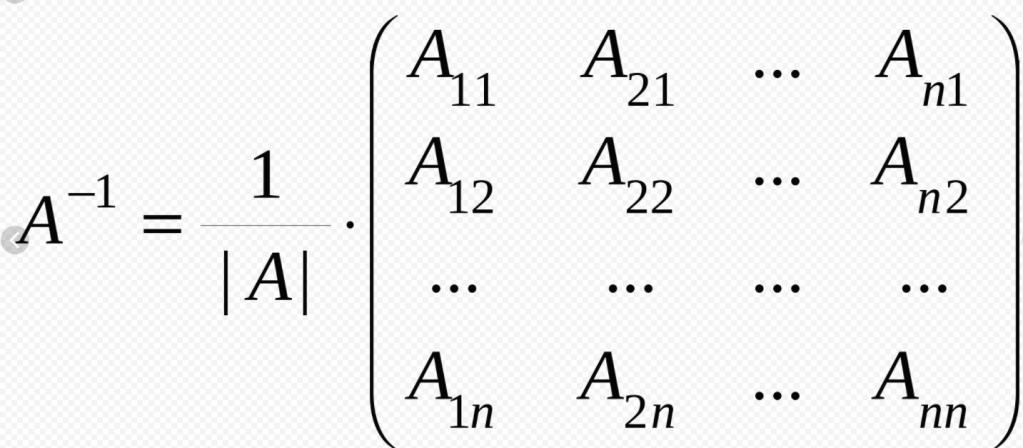
Узнав, что она имеет различные виды, нужно сказать о следующем понятии: ранг матрицы. Под этим подразумевают количество независимых линейных столбцов или же количество независимых линейных строк. Также ранг любой матрицы - это порядок миноров, который является наивысшим, его определитель отличен от нуля.

Обозначается ранг при помощи rang A, но встречается и rank A. Оба понятия считаются правильными, так что при разном написании это не будет считаться ошибкой. Главное не забыть о том, что ранг строк всегда равен рангу столбцов.

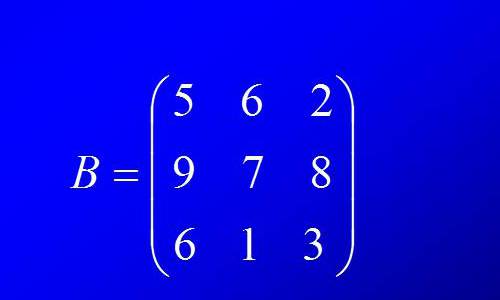
Действия над матрицей

Матрица является универсальной системой решения алгебраических задач, над ней производят различные действия. В их число входит умножение двух матриц, сложение, умножение ее на число и на другие матрицы.

Производя многочисленные действия в алгебре, система различных матриц помогает найти более легкий способ решения поставленных задач. Это отнимает меньше времени и помогает не запутаться в большом количестве действий.

Операции, связанные с матрицей, используются не только в математике, но также и в физике и химии.