Системы счисления: примеры. Перевод систем счисления

Если говорить самым простым языком, система счисления – это способ представления чисел. Мы привыкли использовать при подсчете метод, основанием которого является 10. Другие системы счисления, например, имеют основание 16 (шестнадцатеричная), 8 (восьмеричная) и 2 (двоичная).
Доисторические времена
Подобно тому, как первые попытки писать появились после развития речи, первые усилия по графическому представлению чисел появились после того, как люди научились считать. Вероятно, самый ранний способ вести подсчет – это некая система счета физических объектов, таких как галька или палочки. Судя по обычаям нынешних коренных народов, а также древнейшим следам письменных или скульптурных находок, самые ранние цифры представляли собой простые надрезы на дощечках, царапины на камне, отметки на куске керамики и т. п. Не имея фиксированных единиц измерения, никаких монет, никакой торговли кроме самого примитивного бартера, никакой системы налогообложения и никаких потребностей, помимо тех, которые поддерживали жизнь, люди не нуждались в письменных цифрах до начала так называемых исторических времен.
Первые методы подсчета
Когда стало необходимо часто подсчитывать цифры, превышающие 10, нумерацию необходимо было систематизировать и упростить; это обычно делалось путем использования группы или основы группы. Фактически, самыми ранними записанными цифрами были простые линейные знаки для небольших чисел со специальной формой для 10. Эти символы появились в Египте уже в 3400 году до нашей эры и в Месопотамии уже в 3000 году до нашей эры, на Крите (около 1200 г. до н.э.) и в Индии (около 300 г. до н. э.).
Разумеется, особое место занимает число 10 от количества человеческих пальцев, и это подтверждает современное использование этой основы не только в логической структуре десятичной системы, но и в названиях чисел во многих языках.
Разнообразие методов подсчета
Однако не следует делать вывод, что 10 является либо единственным возможным основанием, либо единственным, фактически используемым. Существует множество примеров систем счисления. Двоичная, в которой подсчет осуществляется «один, два, два и один, два и два, два и два и один» и т. д., встречается среди древнейших племен Австралии, во многих языках народов пролива Торреса и прилегающего берега Новой Гвинеи, среди некоторых африканских пигмеев и в различных южноамериканских племенах. Коренные народы Огненной Земли и Южноамериканского континента используют числовые системы с основаниями три и четыре. Система счисления с основанием пять является очень старой, но в чистом виде она, по-видимому, используется в настоящее время только в некоторых племенах в Южной Америке. В других местах она сочетается с десятичной или двадцатеричной системой, где основание равно 20. Аналогичным образом, система, основанная на 6, редко встречается в северо-западной Африке и связана с двенадцатеричной системой с основанием 12.
В ходе исторического развития десятичная система, наконец, затмила все остальные. Тем не менее есть еще много других систем, которые используются главным образом в коммерческих и бытовых отраслях. Таким образом, основание 12 встречается как число дюймов в футах, месяцев в году, унций в фунте и два раза по 12 часов в день, а также как дюжина, использующаяся при подсчете. Основание 60 встречается при измерении времени и углов.

Цифровые системы
Первыми примитивными цифрами были |, ||, ||| и т. д., например, в Египте и Древней Греции, или -, =, ≡ и т. д., как в Восточной Азии. Такой метод исчисления соответствовал простым потребностям людей. По мере усложнения жизни потребность в количестве групп чисел стала очевидной, и это был всего лишь небольшой шаг от простой системы с наименованиями только для одного и десяти к появлению других специальных чисел, на основании которых можно определить, сколько систем счисления существовало и существует. Иногда этот процесс был бессистемным. Например, юкагиры Сибири считали «один, два, три, три и один, пять, два три, два три и один, два четыре, десять с одним пропущенным, десять». Обычно, однако, более регулярная система приводила к тому, что большинство этих систем можно классифицировать, по крайней мере, в общих чертах, в соответствии с логическими принципами, лежащими в их основе.
Простые системы группировки
Исходя из своего значения, система счисления может рассматриваться как метод группировки чисел. В чистом виде простая система группировки представляет собой назначение особых имен для небольших чисел, базы b и ее полномочий b2, b3 и т. д., до степени bk, достаточной для представления всех чисел, которые действительно необходимы для использования. Промежуточные числа затем формируются путем добавления, каждый символ повторяется требуемое количество раз, так же как 23 написано - XXIII - римскими цифрами.
Самый ранний пример системы счисления такого типа – схема, встречающаяся в египетских иероглифах. Ее использовали древние египтяне для письма на камне.
Позиционные системы счисления
К ним относятся те, в которых позиция (разряд) при записи числа определяет его значение. Система десятичных чисел является примером позиционной системы, в которой после того, как база b была принята, цифрам 1, 2, ..., b-1 присваиваются специальные имена, а все более крупные числа записываются как последовательности этих цифр. Она единственная среди различных систем счисления, которая может использоваться для описания больших чисел. Это обусловлено тем, что каждый из других видов дает специальные имена различным номерам, большим, чем b, и для всех чисел требуется бесконечное число наименований. Успех позиционной системы счисления зависит от того, что для произвольной базы b каждое число N может быть записано единственным образом в виде:
N = anbn + an - 1bn - 1 + ⋯ + a1b + a0,
где a, an - 1, ..., a0 - цифры; то есть числа из группы 0, 1, ..., b - 1. Тогда N в основании b может быть представлено последовательностью символов anan - 1 ... a1a0. Именно этот принцип использовался в мультипликативных системах группировки. Позиционная система проистекает из мультипликативной просто путем исключения имен степеней b, b2 и т. д. и определяется в зависимости от положения цифр для подачи этой информации. Однако тогда необходимо использовать некоторый символ для нуля, чтобы указать любые недостающие полномочия основания; иначе 792 может означать, например, либо 7M9X2 (т. е. 7 092), либо 7C9X2 (792).
Развитие в разных странах
Примером системы счисления такого типа является разработанный вавилонянами метод (примерно 3000-2000 гг. до н. э.). Здесь в качестве основания выступило число 60. Такая система получила название шестидесятеричной. С таким большим основанием было бы неудобно иметь несвязанные наименования для цифр 0, 1, ..., 59, поэтому для этих чисел использовалась простая система группировки до основания 10.
В дополнение к тому, что эта система была громоздкой из-за большого основания, вавилонская система страдала до самого позднего времени от отсутствия обозначения нуля.
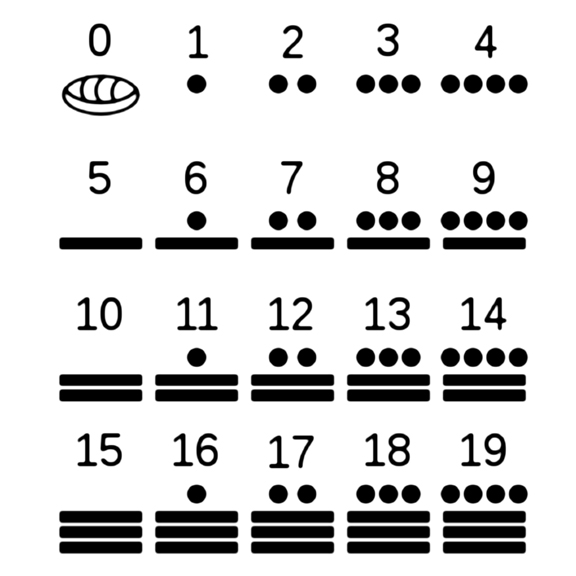
В ходе ранних экспедиций в Юкатан был обнаружен еще один пример системы счисления у майя. Ее использовали, в основном, в календаре, не для коммерческих или других вычислений. Это была хорошо развитая позиционная система. Ее основанием являлось число 20. Цифры 0, 1, ..., 19, как и в Вавилоне, образованы простой системой группировки, в этом случае к основанию 5.
Ни майянская, ни вавилонская система не являются идеальными для арифметических вычислений, потому что цифры менее 20 или 60 не были представлены единичными символами.

Эволюция
Дальнейшее развитие этой идеи связано с индусами, которые также первыми использовали ноль в современном изображении. В позиционных системах необходим некоторый символ, чтобы отметить место, где основание фактически не встречается. Индусы обозначали это точкой или небольшим кругом, которому было дано имя сунья, санскритское слово «пусто». Затем около 800 г. н.э. это обозначение перешло к арабам, причем в переводе значение было сохранено в неизменном виде. После этого его ввели латинский язык (около 1200 года), при этом произношение сохранилось, но значение игнорировалось. Последующие изменения привели к современному обозначению.
Индусско-арабская система
Существует несколько разных мнений в отношении происхождения современных западных цифр: обычно говорят об их арабском происхождении, но предпочтительнее рассматривать индусско-арабское. В этом случае утверждается, что их происхождение связано с арабами, персами, египтянами и индусами. Не исключено, что общение между торговцами служило возможностью переноса этих символов из страны в страну, так что современные западные цифры могут происходить из разных источников. Однако, насколько известно, страной, которая впервые использовала наибольшее кличество этих числовых форм, является Индия. 1, 4 и 6 найдены в надписях Ашоки (III век до н.э.); 2, 4, 6, 7 и 9 появляются в надписях Наны Гат примерно через столетие; и 2, 3, 4, 5, 6, 7 и 9 в пещерах Насика 1-го или 2-го века н.э. Все эти числа имели форму, в значительной степени схожую с сегодняшними.
Преимущества, которыми обладает совершенная система позиционирования, настолько многочисленны и настолько очевидны, что индусско-арабские цифры и основание 10 были приняты почти повсеместно. Можно сказать, что это самый близкий подход к универсальному человеческому языку.
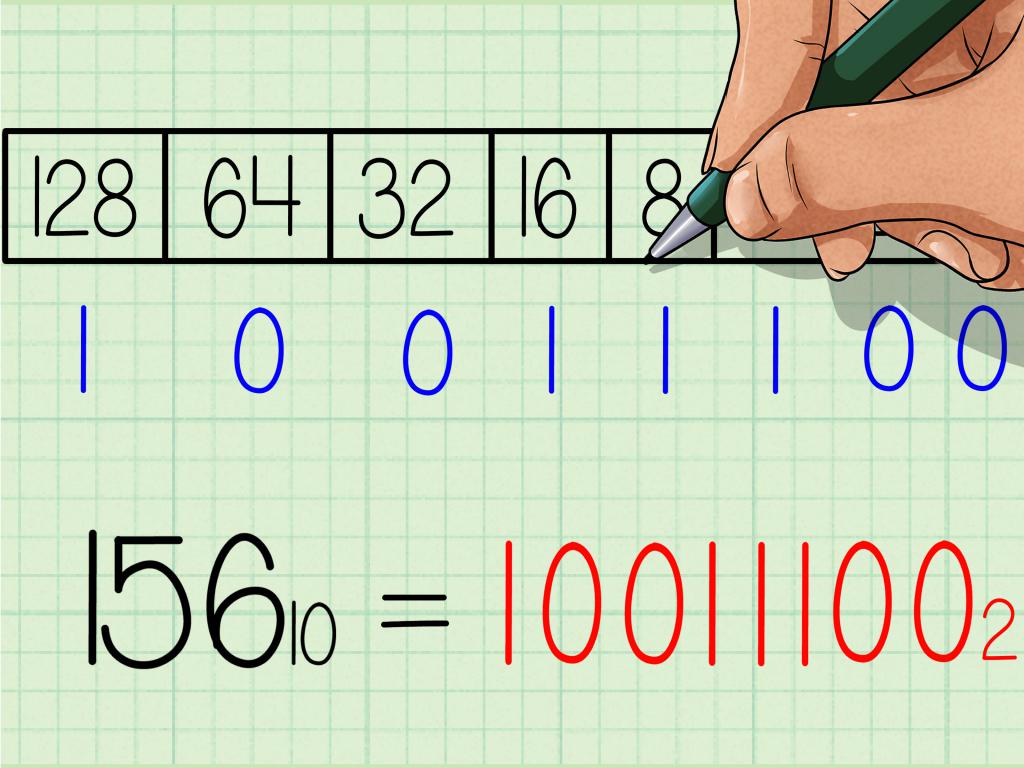
Двоичная система
Однако есть область, в которой привычная десятичная система не является лучшей: компьютер. Здесь двоичная позиционная система имеет больше преимуществ перед десятичной. В этой системе основание 2 определяет, сколько чисел в двоичной системе счисления: здесь всего две цифры – 0 и 1; число два представляется здесь в виде 10, так как оно играет ту же роль, что и десять в десятичной системе.
Двоичное число обычно намного длиннее его соответствующего десятичного числа; например, 256 058 имеет двоичное представление 111 11010 00001 11010. Двоичная цифра, как единица в системе счисления, несет меньше информации, чем десятичная цифра. Причина большей длины двоичного числа состоит в том, что двоичная цифра различает только две возможности: 0 или 1, тогда как десятичная цифра различает 10 возможностей.

Восьмеричная и шестнадцатеричная системы счисления
Их использование также связано с компьютерами и программированием.
Более старая компьютерная система счисления - восьмеричная, где основанием выступает число 8. Цифры, использующиеся в этой системе: 0, 1, 2, 3, 4, 5, 6 и 7. Значение «восемь» записывается как «1 восьмерка и 0 единиц» или 10. Каждое значение позиции отличается от соседней в восемь раз.
С технической точки зрения, существует очень много различных протоколов компьютерного языка для восьмеричной системы.
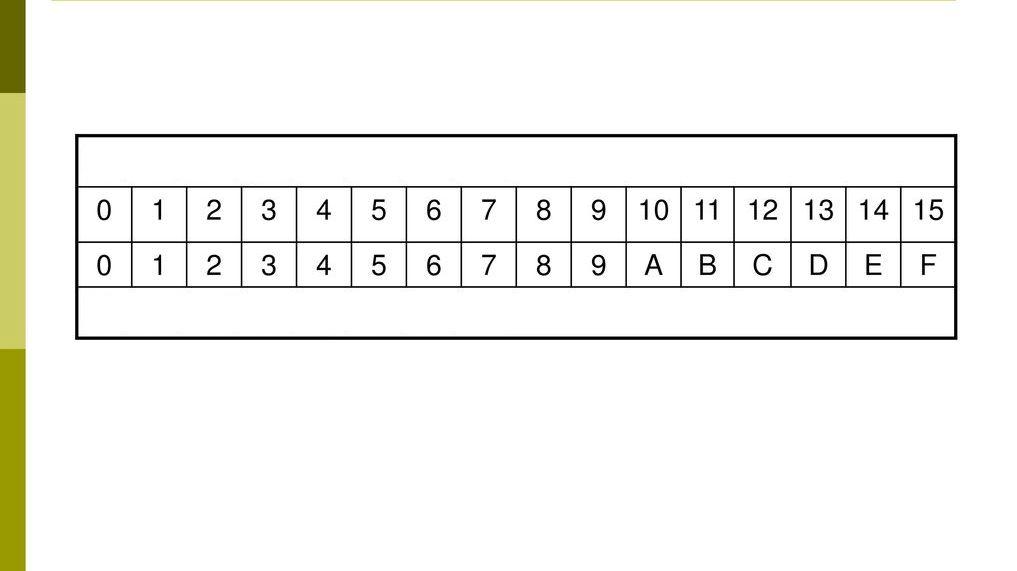
Другая система называется шестнадцатеричной, поскольку это система имеет основание 16. Действующие шифры включают в себя нормальные десятичные символы 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9, а также шесть алфавитных символов A, B, C, D, E и F, что, в общей сложности, составляет шестнадцать. Значение каждой позиции отличается от предыдущей в шестнадцать раз.

Восьмеричная и шестнадцатеричная системы были бы бессмысленными, если бы не их способность легко преобразовываться в двоичную систему и из нее. Их основная цель заключается в том, чтобы служить «сокращенным» методом обозначения числа, представленного электронным способом в двоичной форме. Поскольку основы восьмеричной (8) и шестнадцатеричной (16) систем четные и кратные двоичному основанию (2), двоичные биты могут быть сгруппированы вместе и напрямую произведен перевод чисел в системах счисления в восьмеричные или шестнадцатеричные цифры. При преобразовании в восьмеричную систему бинарные биты группируются в три (потому что 23 = 8), а в шестнадцатеричной - двоичные биты группируются по четыре (потому что 24 = 16).
Аналогично, перевод чисел в системах счисления из восьмеричной или шестнадцатеричной в двоичную выполняется с помощью каждой восьмеричной или шестнадцатеричной цифры и преобразования ее в эквивалентную двоичную (3 или 4-битную) группу, а затем объединяются все группы бит.
Похожие статьи
- Как хоронят мусульманина. Мусульманский обряд похорон
- Закрыть гештальт - что это? Значение и особенности
- Интересные темы для проекта. Проектная деятельность школьников
- Гуманитарные профессии. Профессии социально-гуманитарного профиля
- Где находятся мощи Спиридона Тримифунтского? Феномен нетленных мощей Спиридона Тримифунтского
- Общая характеристика русской литературы 19 века: описание, особенности и интересные факты
- Где живет слепая ясновидящая баба Нина: адрес и отзывы
