Тело бросили под углом к горизонту: скорость, дальность полета и высота подъема

В этой статье рассмотрим анализ ситуации, когда тело бросили под углом к горизонту. Это может быть бросок камня рукой, выстрел снаряда из пушки, запуск стрелы из лука и так далее. Все названные ситуации описываются одинаково с математической точки зрения.

Особенность движения под углом к горизонту

В чем сходство названных выше примеров с точки зрения физики? Оно заключается в характере действующих на тело сил. Во время свободного полета некоторого тела на него действуют всего две силы:

• Сила тяжести.
• Сопротивление воздуха.

Если масса тела достаточно велика, а его форма является заостренной (снаряд, стрела), то сопротивлением воздуха можно пренебречь.

Таким образом, движение брошенного под углом к горизонту тела - это задача, в которой фигурирует только сила тяжести. Именно она и определяет форму траектории, которая с хорошей точностью описывается параболической функцией.

Уравнения движения по параболической траектории. Скорость

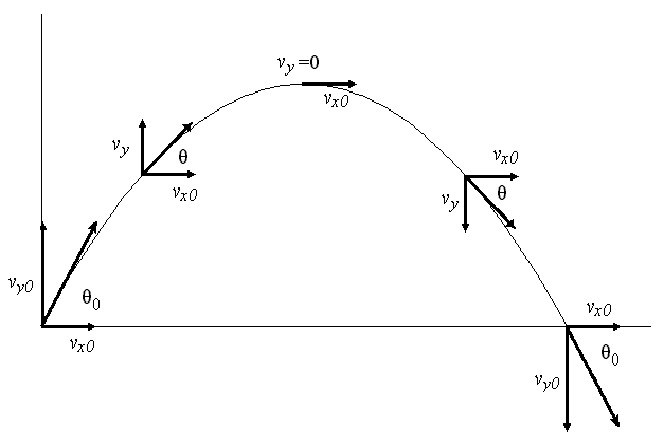
Тело бросили под углом к горизонту. Как можно описать его движение? Поскольку единственная действующая в процессе полета тела сила направлена вниз, то ее горизонтальная составляющая равна нулю. Этот факт означает, что горизонтальное перемещение объекта однозначно определяется начальными условиями (углом броска или выстрела θ и скоростью v). Вертикальное же перемещение тела - это яркий пример равноускоренного движения, где роль ускорения играет постоянная g (9,81 м/с²).

Учитывая сказанное выше, можно записать две компоненты для скорости летящего тела в момент времени t:

v_x = v * cos(θ);

v_y = v * sin(θ) - g * t

Как видно, компонента v_x от времени не зависит и остается постоянной на протяжении всей траектории полета (следствие отсутствия внешних сил в направлении оси x). Компонента же v_y имеет максимум в начальный момент времени. А затем начинает уменьшаться вплоть до того, что обращается в ноль в максимальной точке взлета тела. После этого она изменяет знак и в момент падения оказывается равной модулю начальной компоненты v_y, то есть v*sin(θ).

Записанные уравнения позволяют определить скорость тела, брошенного под углом к горизонту в любой момент t. Ее модуль будет равен:

v = √ (v_x² + v_y²) = √ (v² * cos²(θ) + v² * sin²(θ) - 2 * v* sin(θ) * g * t + g² * t²) =

= √ (v² - 2 * v * sin(θ) * g * t + g² * t²)

Уравнения движения по параболической траектории. Дальность полета

Тело бросили под углом к горизонту. Какое расстояние оно пролетит? Вопрос дальности полета касается изменения координаты x. Найти эту величину можно, если проинтегрировать обе компоненты скорости по времени. В результате интегрирования получаем формулы:

x = v * cos(θ) * t + x₀;

y = v * sin(θ) * t - g * t²/2 + y₀

Разница координат x и x₀ - это и есть дальность полета. Если же положить, что x₀ = 0, тогда дальность будет равна x, для нахождения которой нужно знать, сколько времени t тело будет находиться в воздухе.

Второе уравнение позволяет рассчитать это время при условии, если известна величина y₀ (высота h, с которой бросают тело). Когда объект завершит свое движение (упадет на землю), то его координата y обратится в ноль. Рассчитаем время, когда это произойдет. Имеем:

v * sin(θ) * t - g * t²/2 + h = 0

Перед нами полное квадратное равенство. Решаем его через дискриминант:

D = v² * sin²(θ) - 4 * (-g/2) * h = v² * sin²(θ) + 2 * g * h;

t = (-v * sin(θ) ± √D)/(2 * (-g/2))

Отбрасываем отрицательный корень. Получаем следующее время полета:

t = (v * sin(θ) + √ (v² * sin²(θ) + 2 * g * h))/g

Подставляем теперь это значение в равенство для дальности полета. Получаем:

x = v * cos(θ) * (v * sin(θ)+√ (v² * sin²(θ) + 2 * g * h))/g

Если тело брошено с земли, то есть h = 0, тогда эта формула значительно упростится. И примет вид:

x = 2 * v² * cos(θ) * sin(θ)/g = v² * sin(2 * θ)/g

Последнее выражение было получено с использованием связи между тригонометрическими функциями синуса и косинуса (формулы приведения).

Поскольку синус имеет максимальное значение для прямого угла, тогда максимальная дальность полета достигается, когда тело бросают (выстреливают) с поверхности земли под углом 45°, и эта дальность равна:

x = v²/g

Высота тела, брошенного под углом к горизонту

Теперь определим еще один важный параметр - высоту, на которую способен подняться брошенный объект. Очевидно, что для этого достаточно рассмотреть только изменение координаты y.

Итак, тело бросили под углом к горизонту, на какую высоту оно взлетит? Эта высота будет соответствовать равенству нулю компоненты скорости v_y. Имеем уравнение:

v_y = v * sin(θ) - g * t = 0

Решаем уравнение. Получаем:

t = v * sin(θ)/g

Теперь следует подставить это время в выражение для координаты y. Получаем:

y = v * sin(θ) * t - g * t²/2 + h = v² * sin²(θ)/g - g/2* v² * sin²(θ)/g² + h =

= v² * sin²(θ)/(2 * g) + h

Эта формула свидетельствует о том, что максимальная высота, в отличие от дальности полета, получается, если бросить тело строго вертикально (θ = 90). В этом случае приходим к формуле:

y = v²/(2 * g) + h

Любопытно отметить, что во всех приведенных в этой статье формулах не фигурирует масса тела. Характеристики параболической траектории от нее не зависят, но только в случае отсутствия сопротивления воздуха.