Законы геометрической оптики и их использование в сферических зеркалах и тонких линзах

Поведение световых лучей при их прохождении через различные прозрачные среды можно однозначно определить, не зная при этом природы самого света. Такими задачами занимается особый раздел физики - геометрическая оптика. Законы ее рассматриваются в данной статье.

Свойства световых лучей в геометрической оптике

Под свойствами лучей в этом разделе физики понимают особенности их движения в прозрачных средах. В частности, при перемещении светового пучка в гомогенной среде справедливы следующие утверждения:

• траекторией света является прямая линия;
• два световых пучка, пересекаясь, не взаимодействуют друг с другом;
• вещественная среда определяет скорость движения света в ней.

Эти свойства являются фундаментальными для любой электромагнитной волны. Благодаря им выводятся основные законы геометрической оптики для явлений:

• отражения;
• преломления.

Принцип Ферма

По сути, он является прямым следствием закона прямолинейного распространения света в гомогенном прозрачном материале. Этот принцип устанавливает, что свет во время процессов отражения и преломления выбирает такую траекторию от одной точки к другой в пространстве, которую он сможет преодолеть за наименьшее время.

Принцип наименьшего времени был сформулирован французским ученым Пьером Ферма в начале 1660-х годов. Благодаря принципу Ферма законы геометрической оптики, связанные с явлениями преломления и отражения, получили математическое обоснование. Любопытно отметить, что эти законы уже были известны начиная с 1600-х годов. Что касается Пьера Ферма, то хотя отмеченный принцип наименьшего времени носит его фамилию, сформулирован он был задолго до француза (по крайней мере, для явления отражения). Сделал это греко-египетский философ Герон Александрийский в первый век нашей эры.

Из принципа Ферма однозначно следует, что в гомогенной среде свет должен двигаться по прямой траектории (закон прямолинейного распространения света). Если же среда не является однородной, тогда свет будет распространяться по некоторой кривой, но принцип наименьшего времени нарушаться не будет. Применяя его, можно легко вывести математические формулировки для явлений отражения и преломления, которые были получены благодаря обобщению огромного экспериментального материала.

Процессы преломления и отражение света и их математическое описание

Оба названных явления характеризуются тем, что пучок света в одной точке резко изменяет свою траекторию. Происходит это потому, что в этой точке он встречает препятствие на своем пути. Если это препятствие - материал непрозрачный, тогда происходит единственный процесс отражения. Если же препятствие прозрачное, тогда помимо отраженного луча появляется еще и преломленный.

Предположим, что препятствием является плоская поверхность. Пусть она разделяет две прозрачные среды. Через точку падения луча на поверхность проведем перпендикуляр к ней (нормаль N). Вектор падающего луча обозначим r₁¯, вектор отраженного луча - r₂¯, а преломленного - r₃¯. Угол между r₁¯ и N обозначим θ₁, между r₂¯ и N - θ₂, наконец, между r₃¯ и N - θ₃. Экспериментально установлены следующие соотношения:

1. Вектора лучей r₁¯, r₂¯, r₃¯ и перпендикуляр N лежат в одной плоскости.
2. Угол падения θ₁ и угол отражения θ₂ равны друг другу.
3. Угол преломления θ₃ связан с θ₁ соотношением n₁*sin(θ₁) = n₂*sin(θ₃).

Эта формула называется законом Снелла в честь голландского ученого Виллеброрда Снелла. Сам Снелл получил ее в терминах расстояний. Через синусы углов она была записана несколько позже Рене Декартом, поэтому во франкоговорящих странах она называется законом Снелла - Декарта. Символы n₁ и n₂ - это абсолютные показатели преломления сред, которые определяются отношением скорости света в вакууме к скорости в соответствующем материале.

Отмеченные соотношения принято называть законами отражения и преломления геометрической оптики.

Плоские и сферические зеркала

Закон прямолинейного распространения света и закон отражения используются для геометрических построений изображений в зеркалах. При этом зеркала могут быть не только плоскими, но и выпуклыми, и вогнутыми.

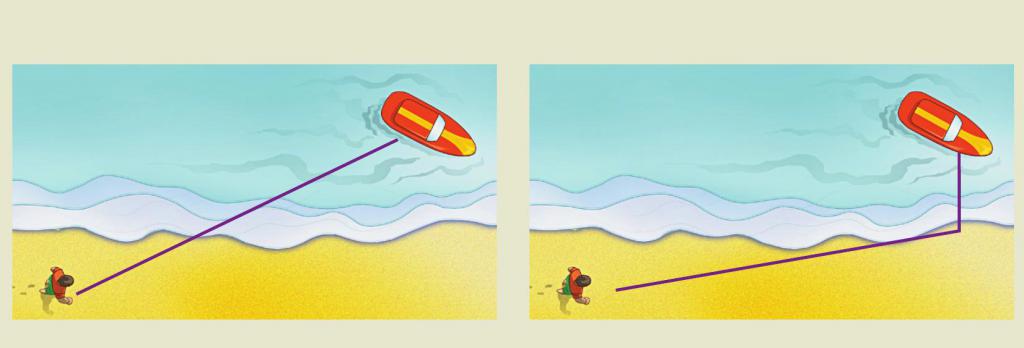
Научиться строить самостоятельно изображения в зеркалах любого типа несложно. Следует лишь понять, как взаимодействуют с оптическим прибором лучи. Так, идущий из фокуса луч всегда отражается зеркалом параллельно оптической оси, а луч, проходящий через центр зеркала (вдоль радиуса), отражается в обратном направлении.

Различные случаи положения объекта относительно оптического прибора и техника построения изображений в вогнутых и выпуклых зеркалах приведены на рисунке ниже.

Тонкие линзы

Это еще один оптический прибор, принцип работы которого базируется на основных законах геометрической оптики. Тонкая линза представляет собой предмет, сделанный из прозрачного материала и ограниченный двумя поверхностями. Одна из поверхностей обязательно должна являться сегментом сферы.

Линзы бывают собирающими (параллельные лучи сходятся в фокусе за линзой) и рассеивающими (мнимые продолжения параллельных лучей сходятся в фокусе перед линзой).

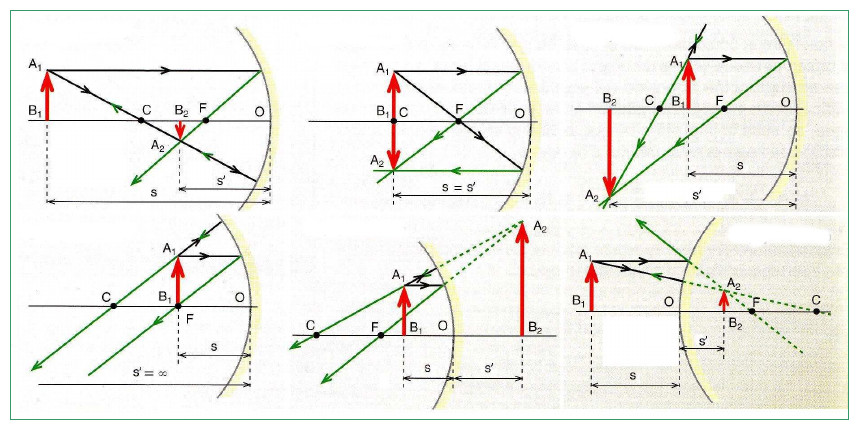
Принцип построения изображений в них практически такой же, как и в сферических зеркалах. Различные случаи показаны на рисунке ниже.

Глаз как оптический прибор

Среди всего прочего законы геометрической оптики используют для изучения принципа работы человеческого глаза и корректировки зрения.

Глаз - это сложная оптическая система с положительной силой, то есть ее можно заменить эквивалентной собирающей линзой. Если аккомодация глаза нарушена (аккомодация приводит к изменения оптической силы глаза, в частности хрусталика), то на сетчатке формируется расплывчатое изображение за счет смещения фокуса за сетчатку (дальнозоркость) или вперед от нее (близорукость). Коррекция осуществляется с помощью добавления (вычитания) диоптрий в глазную систему так, чтобы вернуть фокус на сетчатку. Для этого используют очки, линзы или лазерную коррекцию зрения.