Формула объема шестиугольной призмы правильной. Пример задачи

Рассмотрением свойств и особенностей правильных фигур в трехмерном пространстве занимается стереометрия. Одним из многочисленных классов объемных фигур являются призмы. В данной статье приведем формулу объема призмы шестиугольной и покажем, как ее следует использовать при решении задачи.

Что такое шестиугольная призма?

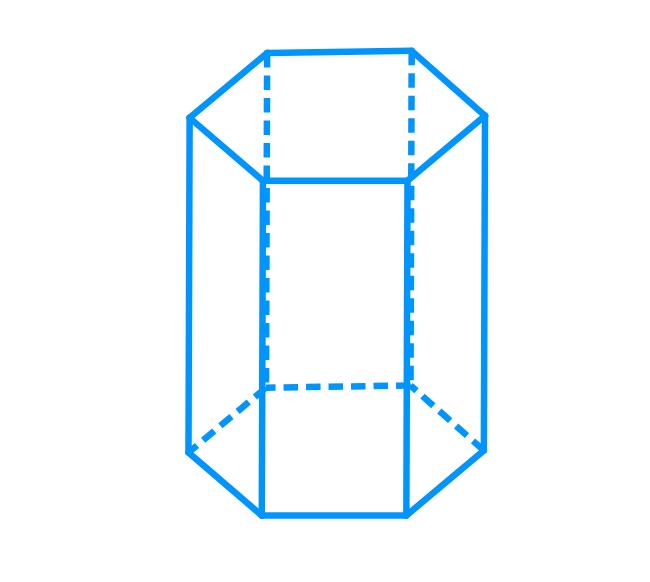
Коротко отвечая на поставленный вопрос, следует сказать, что любая призма, имеющая в основании плоский многоугольник с шестью углами и шестью сторонами, называется шестиугольной. Этот многоугольник называется основанием фигуры. Рисунок ниже показывает, как выглядит такая призма.

Видно, что фигура образована двумя одинаковыми шестиугольными основаниями, которые расположены в параллельных плоскостях. Соединены они с помощью шести параллелограммов. Призма имеет 8 граней, 18 ребер и 12 вершин.

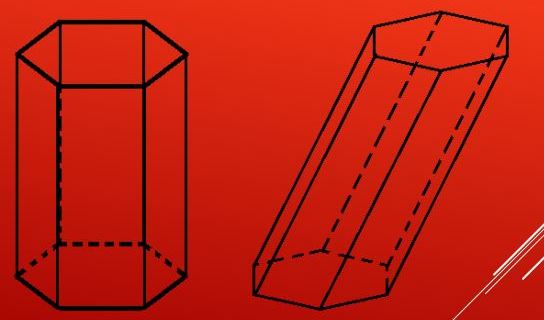
Если все параллелограммы, которые образуют боковую поверхность, представляют собой прямоугольники или квадраты, то фигура будет прямой. У прямой призмы расстояние между основаниями (высота) совпадает с длиной бокового ребра. Если основания прямой фигуры являются равносторонними и равноугольными, то можно говорить о правильной шестиугольной призме.

Определение объема

Теперь ответим на вопрос, как найти объем призмы шестиугольной. Формула для объем произвольной призмы имеет следующий вид:

V = S_o*h

Где S_o - площадь основания, h - высота фигуры. Если мы имеем правильную призму с шестиугольником в основании, то его площадь рассчитать можно, пользуясь следующим выражением:

S_o = 3*√3/2*a²

Где латинской буквой a обозначена длина ребра основания. Это выражение можно получить самостоятельно, если разделить правильный шестиугольник на шесть одинаковых равносторонних треугольников, а затем сложить их площади. Длины сторон треугольников при таком делении будут равны a.

Учитывая выражение для S_o, можно привести формулу объема призмы шестиугольной правильной. Она будет иметь такой вид:

V = 3*√3/2*a²*h

Выражение показывает, что для определения величины V правильной призмы достаточно знать всего два ее линейных размера.

Если в основании прямой фигуры будет находиться неправильный шестиугольник, тогда следует применить геометрический анализ, чтобы определить его площадь S_o.

Самым сложным случаем определения объема шестиугольной призмы является ситуация с наклонной фигурой. Для нее высота уже не равна длине бокового ребра. Чтобы ее вычислить, следует знать какой-либо вертикальный угол (либо между основанием и боковой гранью, либо между ребрами боковым и основания).

Пример задачи

Дана правильная призма шестиугольная. Известно, что ее самая длинная объемная диагональ составляет 25 см. Угол между ней и плоскостью основания составляет 30^o. Чему равен объем геометрической фигуры?

Чтобы воспользоваться полученной выше формулой объема призмы шестиугольной, следует вычислить параметры a и h. Самая длинная объемная диагональ соединяет противоположные вершины разных оснований. Знание ее длины и угла между ней и основанием позволяет вычислить высоту и длину ребра шестиугольника с помощью следующих формул:

a = 25*cos(30^o)/2 = 10,825 см;

h = 25*sin(30^o) = 12,5 см

Теперь можно вычислить V:

V = 3*√3/2*a²*h = 3*√3/2*10,825²*12,5 = 3805,55 см³

Таким образом, искомый объем равен приблизительно 3,8 литра.