Главные линии плоскости - основа геометрии

Главные линии плоскости - это особые прямые, принадлежащие плоскости и позволяющие определить ее положение в пространстве. Давайте разберемся, что это за линии и как их использовать.

Сущность главных линий плоскости

Главными линиями плоскости называют линии уровня (горизонтали и фронтали) и линии наибольшего ската (наклона). Рассмотрим их подробнее.

Линии уровня

Горизонталь - это прямая, принадлежащая плоскости и параллельная горизонтальной плоскости проекций П1. Обозначается буквой h. Горизонтальный след плоскости также является ее горизонталью.

В плоскости можно провести бесконечное множество горизонталей. Это важное свойство, которое часто используется при решении задач.

Фронталь - это прямая, принадлежащая плоскости и параллельная фронтальной плоскости проекций П2. Обозначается буквой f. Фронтальный след плоскости также является ее фронталью.

Как и в случае с горизонталями, в плоскости можно провести бесчисленное множество фронталей.

Линии наибольшего ската

Это линии, принадлежащие плоскости и перпендикулярные ее горизонталям h или фронталям f. С их помощью определяют углы наклона плоскости к плоскостям проекций П1 и П2.

Угол между линией наибольшего ската и ее проекцией как раз и есть искомый угол наклона.

На любой плоскости можно провести бесконечное множество линий наибольшего ската.

Построение главных линий плоскости

Давайте теперь разберем пошаговые алгоритмы построения главных линий для плоскостей, заданных различными способами.

Плоскость, заданная треугольником

Пусть дана плоскость ∆ABC:

1. Выбираем одну из сторон треугольника, например AB
2. Строим горизонталь h параллельно оси Ox (свойство горизонталей)
3. Определяем точку пересечения h со стороной AB - это будет точка D
4. Аналогично строим фронталь f
5. Через точку D проводим линию ската n, перпендикулярную h

Повторив эти действия, можно построить множество главных линий заданной плоскости.

Плоскость, заданная следами

Если плоскость задана следами:

• Берем один из следов в качестве линии уровня (h или f)
• Через точку на следе проводим вторую линию уровня параллельно оси проекций
• Через ту же точку проводим линию ската n, перпендикулярную следу

Таким образом можно построить различные главные линии по заданным следам плоскости.

Как видите, главные линии плоскости - это важный инструмент в начертательной геометрии. Они помогают определить положение плоскости в пространстве, упростить решение многих задач. В следующих частях статьи мы подробно разберем применение главных линий на практике.

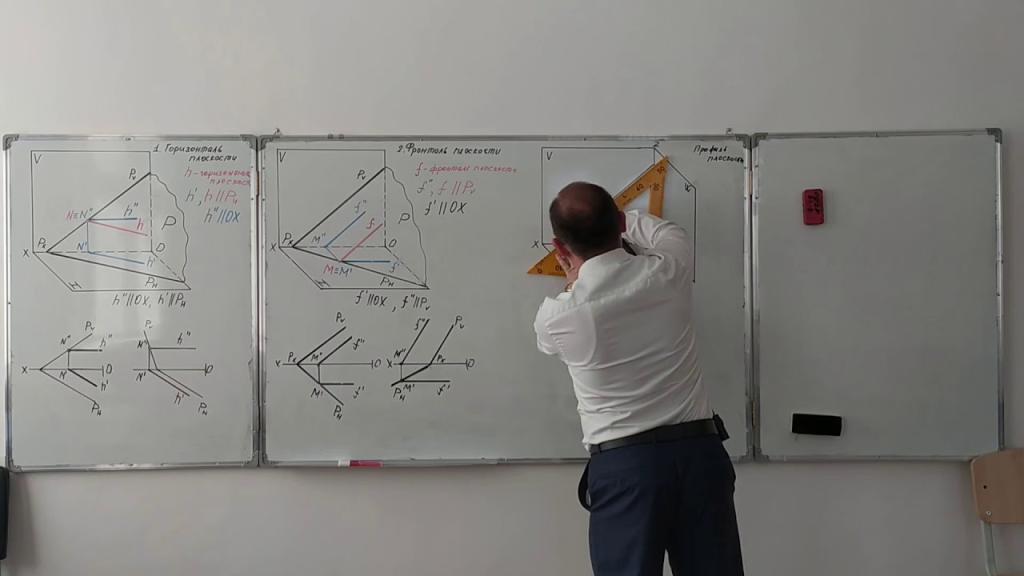
Применение главных линий плоскости

Теперь давайте разберем, как конкретно можно использовать главные линии плоскости для решения различных задач.

Определение положения плоскости в пространстве

Благодаря тому, что линии наибольшего ската образуют с плоскостями проекций известные углы наклона, по ним можно точно определить, как ориентирована заданная плоскость относительно осей координат.

Например, если известен угол φ₁ между линией n и плоскостью П₁, то можно вычислить угол наклона плоскости к оси OZ в градусах или радианах.

Упрощение графических построений

Часто в задачах требуется найти линию пересечения некоторой плоскости с другими объектами - отрезками, плоскостями, многогранниками.

Используя главные линии (особенно горизонтали и фронтали), такие задачи можно свести к нахождению точек пересечения этих линий с искомыми объектами. Это значительно упрощает процесс построения.

Вращение плоскости вокруг ее главных линий

Если представить плоскость в виде диска, то ее можно вращать вокруг различных осей, проходящих через центр этого диска. Удобнее всего брать в качестве таких осей как раз главные линии плоскости.

Например, если вращать плоскость вокруг горизонтали h, то все точки будут двигаться по окружностям, лежащим в параллельных плоскостях.

Преобразования плоских фигур

С помощью вращения вокруг главных линий можно преобразовывать любые фигуры, лежащие на плоскости - многоугольники, кривые, поверхности.

Это позволяет решать такие задачи, как нахождение истинной формы фигуры по ее проекциям, определение видимости отдельных элементов и т.п.

Моделирование сложных поверхностей

Непрерывно вращая различные плоские профили (например, отрезки или сплайны) вокруг главных линий соответствующих плоскостей, можно создавать сложные поверхности - конусы, цилиндры, торы.

Это часто используется в системах автоматизированного проектирования для 3D-моделирования деталей и изделий.

Главные линии плоскости в системах CAD

Давайте теперь разберем, как работать с главными линиями плоскости в популярных САПР.

AutoCAD

В AutoCAD для построения главных линий плоскости используется команда ПЛОСКОСТЬ.

После задания исходной плоскости (например, треугольником), можно вызвать окно свойств этого объекта и указать построение различных линий:

• Горизонтали
• Фронтали
• Линии наибольшего ската

В дополнительных параметрах задается шаг между линиями, что позволяет построить их целую сетку на плоскости.

КОМПАС-3D

В системе КОМПАС трехмерные объекты часто строятся на основе двухмерных эскизов.

Чтобы начертить главные линии в эскизе плоскости, служат инструменты:

1. Линия по сетке
2. Прямоугольник по сетке
3. Круг по сетке

Они автоматически выравнивают объект по горизонталям и фронталям текущей плоскости эскиза.

SolidWorks

Этот CAD позволяет строить главные линии у планарных поверхностей.

Для этого используется команда Главные линии поверхности (Surface Principal Lines) в модуле Деталирование поверхностей.

Можно начертить сразу несколько видов линий с заданным шагом:

• Изолинии гауссовой кривизны
• Линии наименьшей кривизны
• Линии нулевой кривизны

Rhinoceros 3D

В Rhino главные линии для поверхностей часто используются при анализе их геометрии, а также для визуализации в рендере.

Доступны следующие инструменты:

• Показать изолинии кривизны
• Скрыть изолинии кривизны
• Показать направления кривизны

Причем линии кривизны будут автоматически пересчитываться при любых модификациях поверхности.