Найти
×

Лемниската Бернулли: график, уравнение

0
0

Лемниската Бернулли - удивительная математическая кривая с богатой историей. Она была открыта великим швейцарским математиком Якобом Бернулли в 1694 году. С тех пор лемниската привлекает к себе внимание математиков своей элегантной формой, напоминающей восьмерку, и множеством интересных свойств.

Определение лемнискаты Бернулли

Лемниската Бернулли определяется как геометрическое место точек, произведение расстояний от которых до двух фиксированных точек (фокусов) постоянно и равно квадрату полурасстояния между фокусами. Формально:

  • Пусть F1 и F2 - две фиксированные точки (фокусы)
  • Пусть 2c - расстояние между фокусами
  • Тогда множество точек M, для которых выполняется соотношение MF1 * MF2 = c2, и есть лемниската Бернулли

Это определение задает лемнискату в неявном виде. Чтобы получить явное уравнение в декартовых или полярных координатах, нужно выполнить ряд преобразований, о которых речь пойдет ниже.

История открытия

Лемниската Бернулли была впервые описана в 1694 году швейцарским математиком Якобом Бернулли в его работе "Curvatura laminae elasticae" (Кривизна упругой пластины). Бернулли дал этой кривой название "lemnisce" на латыни, что означает "ленточка".

"Я нашел линию удивительной красоты, которую назвал лентой или лемниской" (Якоб Бернулли)

Хотя лемниската и была открыта Бернулли, но она является частным случаем более общего семейства кривых - овалов Кассини, описанных Джованни Кассини за 14 лет до этого, в 1680 году.

бернулли лемниската

Уравнения лемнискаты Бернулли

Рассмотрим простейший случай, когда фокусы лемнискаты лежат на оси OX, а начало координат находится в середине между ними. Тогда в прямоугольных и полярных координатах лемниската имеет следующий вид:

  1. Прямоугольные координаты: (x2 + y2)2 - 2a2(x2 - y2) = 0 где a - радиус окружности, описанной вокруг лемнискаты
  2. Полярные координаты: r2 = 2a2cos(2φ)

Эти уравнения можно получить из определения лемнискаты, выполнив ряд преобразований. Подробные выводы представлены в соответствующем разделе.

Чтобы задать лемнискату для двух произвольно расположенных фокусов F1(x1, y1) и F2(x2, y2), нужно выполнить следующие действия:

  1. Найти координаты центра O(x0, y0) как середину отрезка F1F2
  2. Повернуть систему координат так, чтобы ось OX совпала с F1F2
  3. Подставить преобразованные координаты в стандартные уравнения выше

В результате мы получим уравнение лемнискаты Бернулли для произвольно заданных фокальных точек.

Способы построения лемнискаты Бернулли

Существует несколько методов построения лемнискаты Бернулли.

Построение с помощью циркуля и линейки

Наиболее простой способ - использование циркуля и линейки. Для этого:

  1. Отмечаем на линии две точки F1 и F2, задающие фокусы
  2. С помощью циркуля, используя F1 и F2 как центры, проводим дуги различного радиуса
  3. Точки пересечения этих дуг и образуют лемнискату Бернулли. График:
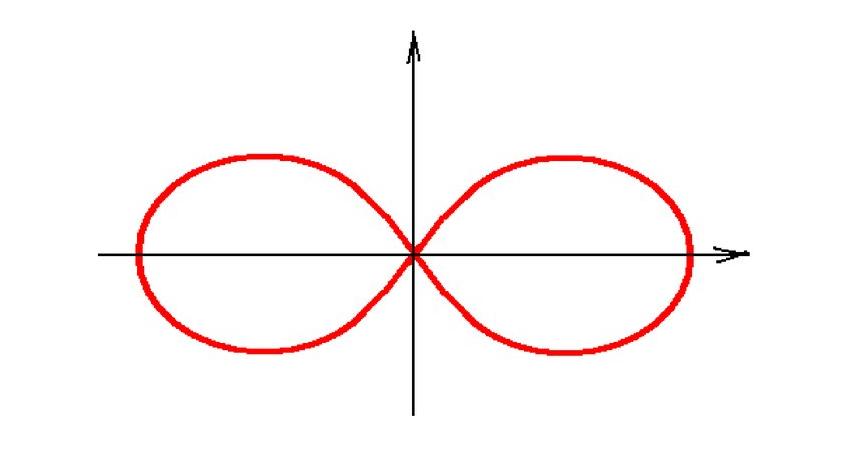
    бернулли лемниската

Построение по точкам

Лемнискату можно построить, зная координаты нескольких ее точек. Алгоритм:

  1. Находим 5-7 точек, принадлежащих лемнискате
  2. Строим график этих точек с помощью линейки
  3. Через полученные точки проводим плавную кривую - лемнискату

Построение по уравнению

Зная уравнение лемнискаты в декартовых координатах, ее легко построить:

  1. Задаем сетку значений x и y с некоторым шагом
  2. Подставляем значения x и y в уравнение лемнискаты
  3. Вычисляем значения y при заданных x, удовлетворяющие уравнению
  4. Строим точки с координатами (x, y) - получаем график лемнискаты

Построение в полярных координатах

Алгоритм аналогичен построению в декартовых координатах, но использует уравнение лемнискаты в полярной системе координат.

Построение с помощью компьютерных программ

Существует множество специализированных математических пакетов, позволяющих строить графики различных кривых, в том числе лемнискаты Бернулли. Наиболее популярные из них:

  • Mathematica
  • Maple
  • Mathcad
  • GeoGebra

Для построения лемнискаты в этих программах достаточно ввести ее уравнение и задать диапазон изменения переменных. Программа автоматически выстроит график.

Построение в трехмерном пространстве

Лемнискату можно построить не только на плоскости, но и в трехмерном пространстве. Для этого используют:

  • Тор, образуемый вращением лемнискаты вокруг оси симметрии
  • Эллипсоид вращения, огибающий лемнискату

Такие 3D-модели лемнискаты наглядно демонстрируют ее свойства и позволяют изучать эту удивительную кривую с разных сторон буквально.

Физические модели

Для наглядного представления лемнискаты используют также физические модели. Их можно изготовить из:

  • Проволоки
  • Резины
  • Дерева
  • Пластика

Такие модели обычно крепятся на подставке с двумя гвоздями, обозначающими фокусы. Натягивая резинку или проволоку через эти "фокусы", можно легко получить материальный аналог лемнискаты.


Похожие статьи