Тангенс угла - это отношение, определяющее тригонометрические функции
Тригонометрия является фундаментальным разделом математики, позволяющим решать множество прикладных задач в самых разных областях. Одно из ключевых понятий тригонометрии - тангенс угла. Давайте разберемся, что оно означает и почему так важно.
История возникновения понятия "тангенс угла"
Слово "тангенс" произошло от латинского "tangens", означающего "касающийся". Изначально это понятие применялось в геометрии для нахождения касательной к заданной кривой.
В дальнейшем, с развитием тригонометрии в трудах античных (Евклид, Архимед) и средневековых (Ариабхата, арабские математики) ученых, термин "тангенс" стал использоваться для обозначения отношения sine к cosine и закрепился в этом значении.
Тангенс угла в прямоугольном треугольнике
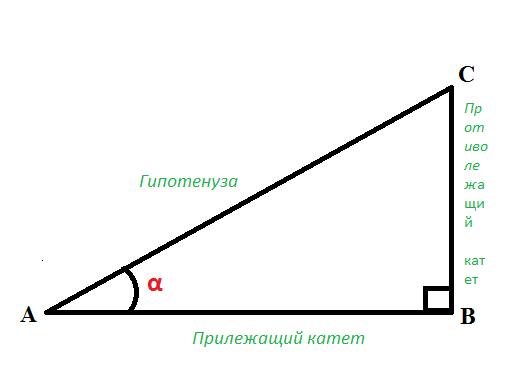
Рассмотрим прямоугольный треугольник ABC с прямым углом C (рис. 1):
Тогда тангенсом угла A называется отношение длины противолежащего катета BC к длине прилежащего катета AB:
tgA = BC/AB
Аналогично для угла B:
tgB = AB/BC
Тангенс угла в прямоугольном треугольнике это отношение противолежащего катета к прилежащему.
Пользуясь этим определением, можно находить тангенсы острых углов в прямоугольном треугольнике, зная соотношение его сторон. Например, в равнобедренном прямоугольном треугольнике тангенс острого угла равен 1.
Кроме того, из определения тангенса следует важное свойство:
tg(90° - A) = 1/tgA
То есть тангенс дополнительного угла равен котангенсу данного угла. Это позволяет находить тангенс одного из острых углов, зная тангенс другого.
Вычисление тангенсов острых углов в прямоугольном треугольнике
Рассмотрим конкретный пример. Дан прямоугольный треугольник с катетами 3 и 4 (рис. 2). Найдем тангенс острого угла A:
Противолежащий катет равен 4, прилежащий катет равен 3. Подставляя значения в формулу, получаем:
tgA = 4/3
Аналогично можно вычислить тангенс угла B:
tgB = 3/4
Нахождение углов и сторон треугольника по тангенсу
Зная тангенс острого угла прямоугольного треугольника, можно найти сам угол, а также длины сторон triangles. Для этого используются обратные тригонометрические функции:
- арктангенс для нахождения угла:
A = arctgA - длину гипотенузы можно найти по теореме Пифагора

Применение тангенса в технических расчетах
Отношение сторон в прямоугольном треугольнике используется в различных технических задачах, где важны углы наклона или ориентации объекта:
- Расчет рамп, откосов
- Определение высоты объектов по тени
- Расчет нагрузок на опоры
Тангенс угла в прямоугольном треугольнике: достоинства и недостатки
Использование определения тангенса как отношения катетов в прямоугольном треугольнике имеет следующие плюсы и минусы:
| Плюсы | Недостатки |
| - Простота и наглядность | - Применимо только для острых углов в прямоугольном треугольнике |
| - Легкость вычисления по известным сторонам | - Неудобно для нахождения самих сторон или углов по заданному тангенсу |
Тангенс угла как отношение тригонометрических функций
Помимо определения через катеты прямоугольного треугольника, тангенс можно задать как отношение двух других тригонометрических функций:
tgα = sinα/cosα
Где α - угол, sinα - синус этого угла, cosα - косинус.
Вычисление тангенса по значениям синуса и косинуса
Используя формулу tgα = sinα/cosα, можно вычислить тангенс угла, если известны его синус и косинус. Например:
sinα = 0.6, cosα = 0.8. Тогда:
tgα = sinα/cosα = 0.6/0.8 = 0.75
Определение синуса, косинуса и тангенса через точки на окружности
Синус, косинус и тангенс угла можно также определить геометрически - через координаты точки на единичной окружности, полученной поворотом на данный угол.
Это позволяет наглядно представить тригонометрические функции и их взаимосвязь.
Построение тангенса по единичной окружности
Зная расположение синусоиды и косинусоиды на единичной окружности, тангенс любого угла можно построить геометрически как отношение соответствующих отрезков, отсекаемых этими кривыми от осей координат.
Это наглядный способ определения тангенса, не требующий вычислений.
Применение формул тангенса в тригонометрических преобразованиях
Благодаря формуле tgα = sinα/cosα, многие тригонометрические выражения можно упростить, привести к виду, удобному для дальнейшей работы. Это часто используется при решении уравнений, доказательстве тождеств и т.д.
Значения тангенсов некоторых углов
Тангенсы некоторых углов, встречающихся часто при решении задач, запомнить полезно.
- tg0° = 0
- tg30° = 1/√3
- tg45° = 1
- tg60° = √3
- tg90° = не определен (угол прямой)
Мнемонические правила
Чтобы легче запомнить значения тангенсов, используют различные мнемонические приемы, например "правило на ладони":
Построение тангенсов по единичной окружности
Зная расположение линий тангенсов и котангенсов на единичной окружности, можно графически определить тангенс заданного угла, не прибегая к вычислениям.
Применение известных значений тангенсов
Знание точных значений tg30°, tg45° и tg60° позволяет оперативно решать задачи с участием данных углов, не тратя время на вычисления.
Использование таблиц значений
Для остальных углов удобно пользоваться таблицами значений тангенса, синуса и косинуса. Это избавляет от необходимости каждый раз проводить вычисления заново.
Тригонометрические уравнения, содержащие тангенс
С помощью тангенса можно решать разнообразные тригонометрические уравнения.
Методы решения простейших тригонометрических уравнений
Рассмотрим решение простейшего уравнения вида:
tgx = a
где a - некоторое число.
Для этого используем обратную тригонометрическую функцию - арктангенс. Тогда решением будет уравнение:
x = arctg a
Аналогично можно решать уравнения для ctgx, sinx и cosx.
Более сложные тригонометрические уравнения
Рассмотрим несколько примеров более сложных тригонометрических уравнений, содержащих тангенс:
- tg2x + tgx = 0
- tgx - ctgx = 3
- 2tgx + √3 = 5
Для решения таких уравнений применяются различные методы и тождественные преобразования.
При изучении математического анализа важно уметь находить производную от различных функций, в том числе от тангенса.
Похожие статьи
- Где находятся мощи Спиридона Тримифунтского? Феномен нетленных мощей Спиридона Тримифунтского
- История Кёсем Султан: биография, правление и интересные факты
- Специальность "Технология машиностроения". Кем можно работать?
- Какие бывают предложения по цели высказывания и по интонации? Виды предложений по цели высказывания
- И. Бунин "Одиночество": анализ стихотворения по плану
- Многочлены. Разложение многочлена на множители: способы, примеры
- Парные и непарные, звонкие и глухие, мягкие и твердые согласные звуки в русском языке
