Что такое отрезки в геометрии и для чего они нужны?
Отрезки являются одним из фундаментальных понятий геометрии. Их изучение позволяет решать множество задач, связанных с измерениями, вычислениями и построениями. Давайте разберемся, что представляет собой отрезок и почему он так важен в геометрии.
Определение отрезка
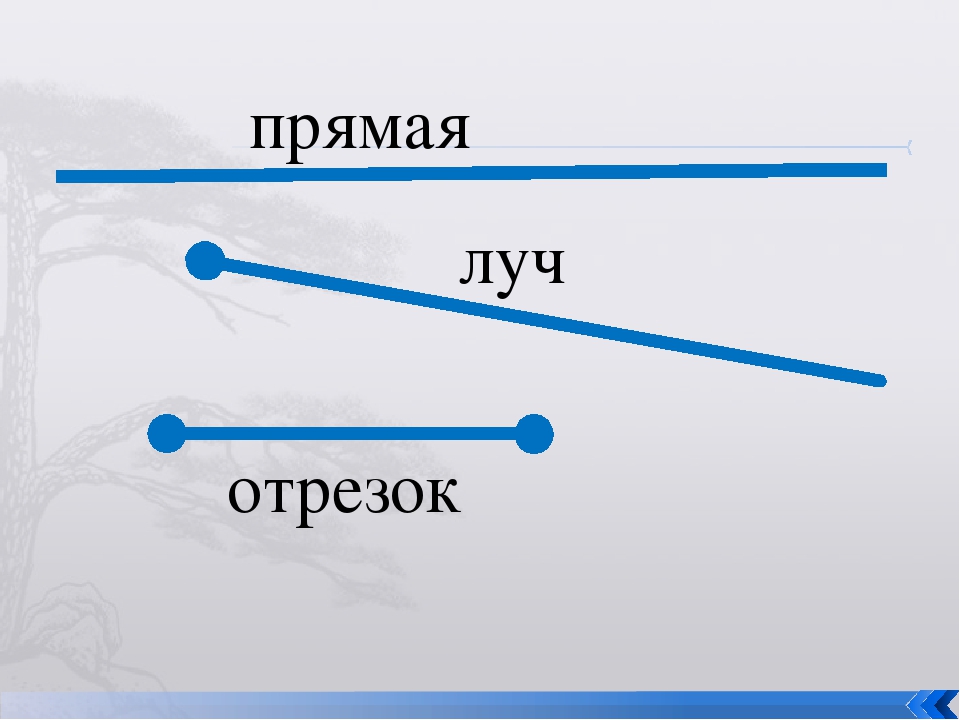
Отрезок — это часть прямой, ограниченная с двух сторон точками. Эти точки называются концами отрезка . Расстояние между ними определяет длину отрезка .
Формальное определение выглядит так:
Отрезок AB — это множество точек прямой AB, лежащих между точками A и B.
Главное отличие отрезка от прямой или луча в том, что он имеет конечную длину. Это позволяет использовать отрезки для измерений и вычислений в геометрических задачах.
Свойства отрезка
У отрезков есть несколько важных свойств:
- Отрезок имеет определенную длину
- Через две точки можно провести только один отрезок
- Отрезок может быть разделен на части другими точками
- Отрезки могут быть равны, если их длины совпадают
Эти свойства позволяют выполнять с отрезками разнообразные операции, необходимые для решения многих геометрических задач.
Применение отрезков в геометрии
Благодаря своим свойствам, отрезки широко используются в различных областях геометрии.
Вот лишь некоторые примеры:
- Построение геометрических фигур (треугольников, четырехугольников и др.)
- Вычисление периметров и площадей
- Решение задач на доказательство и вычисление
- Моделирование реальных объектов и процессов
Рассмотрим более подробно некоторые случаи.
Построение геометрических фигур
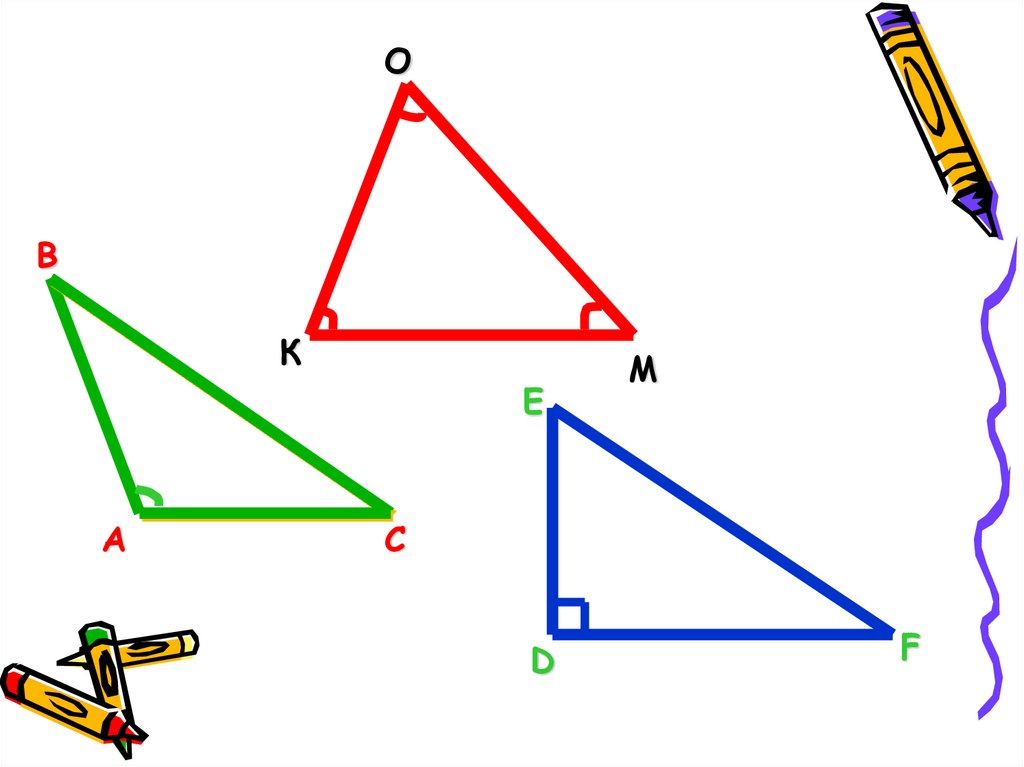
Многие фигуры (треугольники, четырехугольники, многоугольники) строятся из отрезков. Например, для построения треугольника достаточно задать длины его трех сторон — отрезков AB, BC и CA:
| Сторона | Длина |
| AB | 5 см |
| BC | 7 см |
| CA | 6 см |
Используя эти данные и методы геометрических построений, можно получить искомый треугольник ABC.
Вычисление периметров и площадей
Периметр многоугольника равен сумме длин всех его сторон, а стороны представляют собой отрезки. Таким образом, зная длины отрезков, образующих контур многоугольника, можно найти его периметр.
Аналогично, площади многих фигур (прямоугольник, параллелограмм, трапеция) выражаются через длины их сторон — отрезков.
Построение четырехугольников
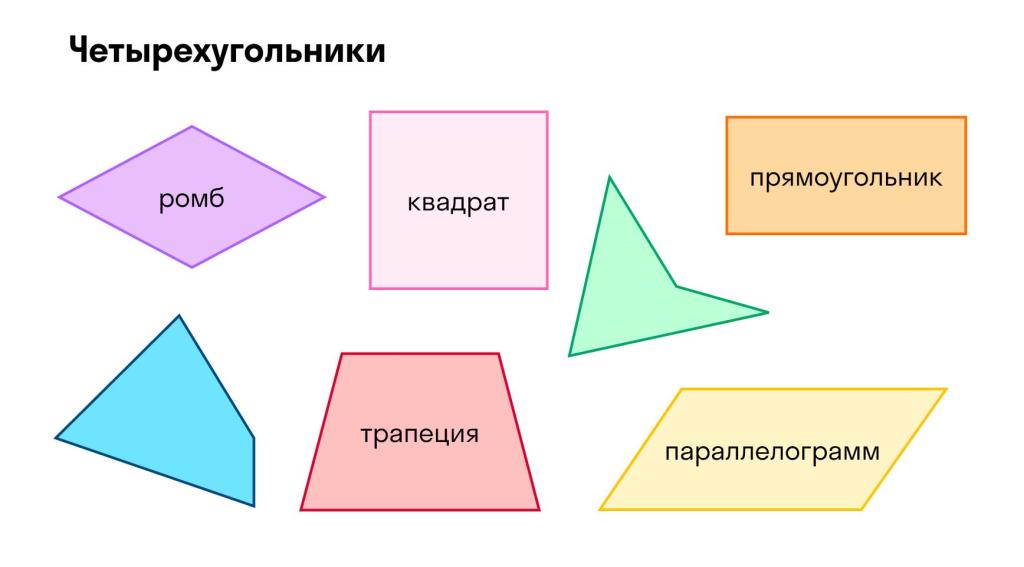
Четырехугольник задается четырьмя отрезками - его сторонами. Помимо длин сторон, для однозначного построения четырехугольника также необходимы:
- Три стороны и два угла, образованные этими сторонами
- Две стороны и три угла
- Диагонали четырехугольника
Зная это, можно использовать отрезки для построения таких четырехугольников как прямоугольник, параллелограмм, ромб, трапеция и др.
Что такое отрезки в геометрии: резюме
Итак, отрезок — это конечный фрагмент прямой линии, заключенный между двумя точками (вершинами). Определяя длину отрезков, строя из них различные фигуры, сравнивая и вычисляя, мы можем решать множество задач геометрии.
Важность отрезков в геометрии трудно переоценить. Фактически, этим простым понятием задается базис, фундамент для изучения всех остальных объектов и их свойств.
Понимание того, что такое отрезки в геометрии , позволяет двигаться дальше — к изучению углов, треугольников, четырехугольников и окружностей. А на основании этих знаний решать сложные задачи на вычисление, доказательство и построение.
Похожие статьи
- Какие бывают предложения по цели высказывания и по интонации? Виды предложений по цели высказывания
- Первопечатник Иван Федоров: биография краткая для детей
- Мифы Древней Греции: краткое содержание и суть
- Тригонометрия с нуля: основные понятия, история
- Особенности российской модернизации начала 20 века. История России
- Легенда и миф о Зевсе кратко для учащихся 5 класса
- Известные русские химики: список, достижения, открытия и интересные факты
