Прямоугольник: свойства, признаки, определение, отличия

Прямоугольник - одна из самых распространенных геометрических фигур. Мы сталкиваемся с ней повсюду: окна, двери, столы имеют форму прямоугольника. Давайте разберемся, что представляет собой эта удивительная фигура, какие у нее свойства и отличительные признаки. Итак, начнем с определения.

Определение прямоугольника

Итак, давайте начнем с формального определения:

Прямоугольник – это четырехугольник, у которого все углы прямые и равны 90°.

Геометрически это означает, что прямоугольник образован двумя парами параллельных сторон, пересекающихся под прямым углом.

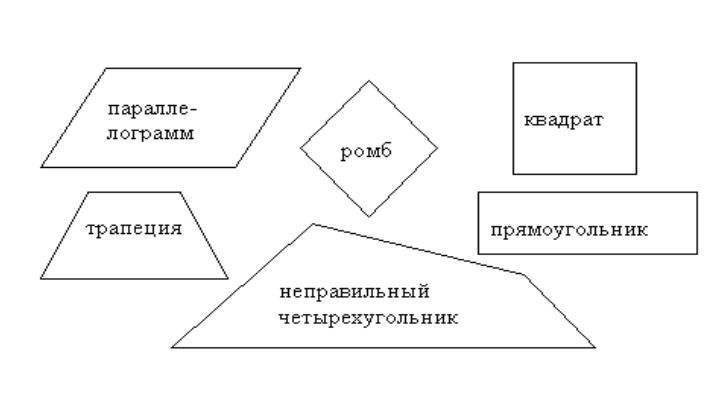
Прямоугольник является частным случаем параллелограмма. У него есть "родственники" среди других геометрических фигур (см. рисунок)

Примеры прямоугольников в окружающем мире

В нашей повседневной жизни мы постоянно сталкиваемся с предметами, имеющими форму прямоугольника:

1. Листы бумаги, тетради
2. Оконные и дверные проемы
3. Экраны телевизоров и мониторов
4. Столы, парты
5. Книги, журналы

История открытия свойств прямоугольника

Интересный факт: свойства прямоугольника впервые были сформулированы и доказаны еще в Древней Греции математиком Евклидом в его знаменитых "Началах". С тех пор они не менялись уже более 2000 лет!

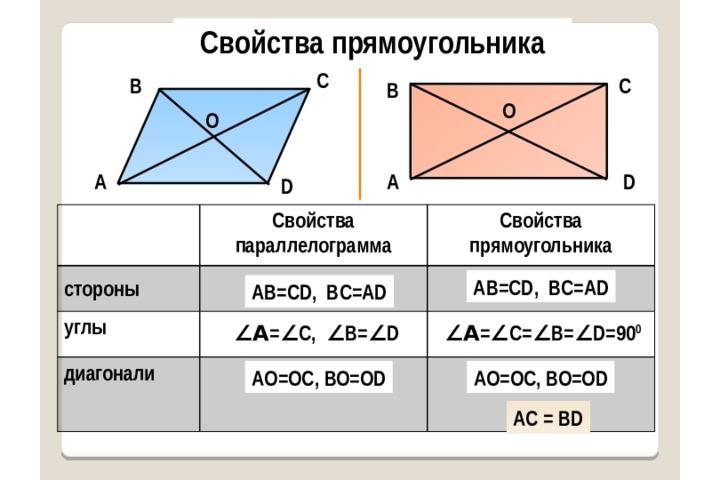
Свойства параллелограмма

Поскольку прямоугольник является частным случаем параллелограмма, то на него распространяются все свойства параллелограмма:

• Противоположные стороны параллельны и равны
• Диагонали взаимно перпендикулярны (пересекаются под прямым углом)
• Диагонали делят параллелограмм пополам

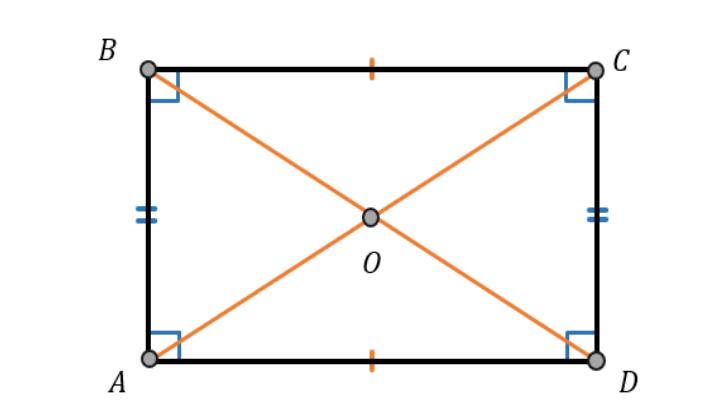
Собственные свойства прямоугольника

Кроме того, у прямоугольника есть и свои, "фирменные" свойства:

1. Все углы прямые и равны 90°
2. Диагонали равны

Применение свойств прямоугольника на практике

Свойства прямоугольника широко используются на практике:

• При решении задач на вычисление площади
• В строительстве прямоугольных конструкций

Сравнение свойств прямоугольника, квадрата и ромба

Свойства прямоугольника отличаются от свойств квадрата и ромба. К примеру, у ромба диагонали взаимно перпендикулярны, но не равны. А у квадрата стороны не только равны, но и являются биссектрисами углов.

Признаки прямоугольника

Для того чтобы отличить прямоугольник от других четырехугольников, используются специальные признаки. Рассмотрим 3 основных признака.

1. Признак параллельности: если в четырехугольнике две смежные стороны равны, а две другие параллельны, то это прямоугольник
Copy code
2. Признак перпендикулярности: если диагональ четырехугольника делит его пополам и перпендикулярна второй диагонали, то это прямоугольник

Сравнение признаков прямоугольника, квадрата и ромба

Признаки прямоугольника также отличаются от признаков квадрата и ромба. Например, у квадрата все стороны равны, а у ромба диагонали взаимно перпендикулярны.

Доказательства признаков прямоугольника

Давайте докажем один из признаков прямоугольника - признак параллельности. Рассмотрим четырехугольник ABCD, у которого AB = CD и AD параллельно BC. Проведем диагональ BD. Так как ABCD - параллелограмм, то BD перпендикулярна AD и BC. Кроме того, треугольники ABD и CBD равны по двум сторонам и углу между ними, значит, они равны. Следовательно, углы ABD и CBD прямые, а так как в параллелограммах противоположные углы равны, то ABCD - прямоугольник.