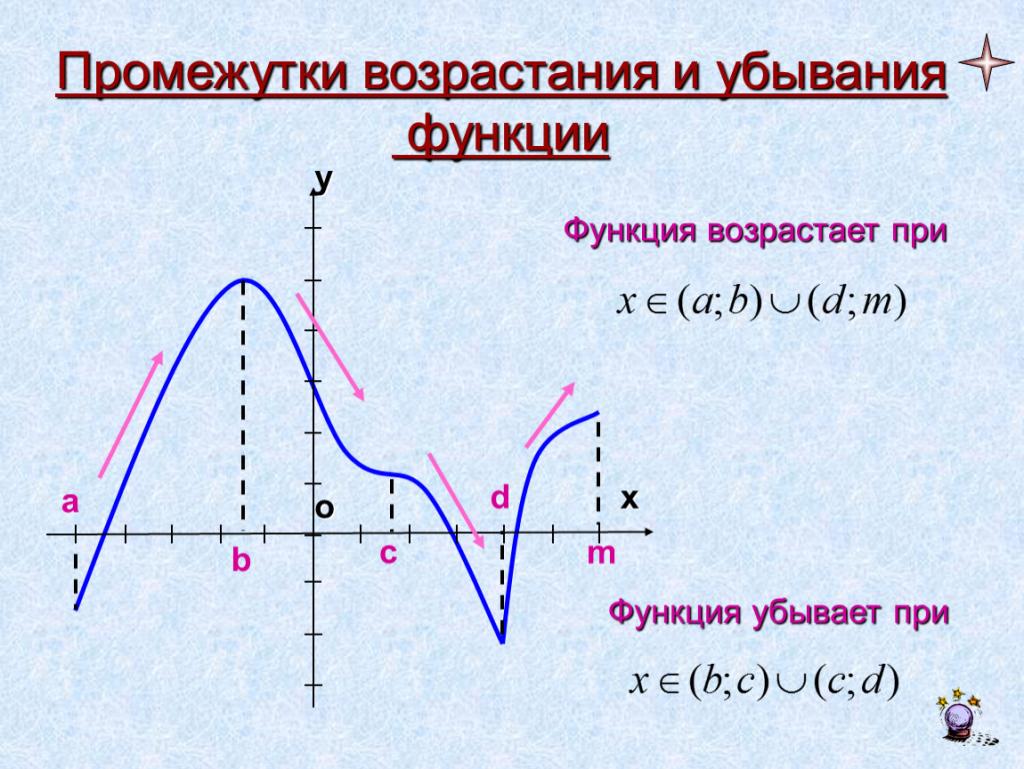
Промежутки возрастания и убывания функции: свойства функции

Функция является важным математическим понятием, описывающим зависимость одной переменной от другой. Одним из ключевых свойств функции является ее монотонность - способность либо возрастать, либо убывать. Рассмотрим подробно, что такое промежутки возрастания и убывания функции , как их находить и для чего они нужны.

Определение возрастания и убывания функции
Функция y = f(x) называется возрастающей на промежутке (a; b), если выполняется условие:
- для любых двух точек
x1иx2принадлежащих этому промежутку, таких чтоx1 < x2 - выполняется неравенство
f(x1) < f(x2)
Иначе говоря, на промежутке возрастания бóльшему значению аргумента соответствует бóльшее значение функции. Графически это выглядит как восходящая кривая слева направо.
Аналогично, функция y = f(x) называется убывающей на промежутке (a; b), если:
- для любых двух точек
x1иx2принадлежащих этому промежутку, таких чтоx1 < x2 - выполняется неравенство
f(x1) > f(x2)
Здесь, наоборот, бóльшему значению аргумента соответствует мéньшее значение функции. Графически это нисходящая кривая.
Как найти промежутки возрастания и убывания
Чтобы определить, где функция возрастает, а где убывает, нужно:
- Найти производную функции
f'(x) - Найти промежутки, где
f'(x) > 0(функция возрастает) - Найти промежутки, где
f'(x) < 0(функция убывает)
Этот метод называется признаком возрастания и убывания функции. Он работает, если функция дифференцируема на данном промежутке.
Например, для функцииf(x) = 3x2 - 2xпроизводная равнаf'(x) = 6x - 2. Ставимf'(x) > 0и получаем промежуток возрастания(1/3; +∞), где функция растет. А приf'(x) < 0имеем промежуток убывания(-∞; 1/3).
Зачем нужны промежутки монотонности
Знание интервалов возрастания и убывания функции позволяет решать такие задачи:
- Находить наибольшее и наименьшее значение функции на отрезке
- Исследовать функцию на экстремумы
- Строить график функции
- Описывать качественные свойства процессов в физике, экономике и других науках с помощью графиков
Например, если известно, что некоторая физическая величина, зависящая от x, возрастает на интервале (2; 5) и убывает на интервале (6; 10), то мы можем сделать выводы о поведении этого процесса при разных x.
Таким образом, промежутки монотонности - это важное свойство функций, позволяющее решать множество прикладных задач.
Признак возрастания и убывания в действии
Рассмотрим на конкретном примере, как применяется признак возрастания убывания функции для нахождения интервалов монотонности функции f(x) = x^3 - 6x^2 + 9x.
- Находим производную:
f'(x) = 3x^2 - 12x + 9 - Приравниваем производную к нулю:
3x^2 - 12x + 9 = 0 - Решаем это уравнение и находим критические точки
x1 = 1,x2 = 3
Теперь применяем признак: подставляем в производную некоторые значения x слева и справа от каждой критической точки и смотрим ее знак:
Copy codeCopy code
| Промежуток | Значение f'(x) | Вывод |
| x < 1 | f'(0) = 9 > 0 | Функция возрастает |
| 1 < x < 3 | f'(2) = -6 < 0 | Функция убывает |
| x > 3 | f'(4) = 15 > 0 | Функция возрастает |
Итого, функция возрастает на интервалах (-∞; 1) и (3; +∞), убывает на интервале (1; 3). Признак возрастания и убывания позволил легко это установить.
Связь с физическими процессами
Промежутки монотонности позволяют описывать зависимости величин в физике, химии, экономике. Например, пусть зависимость скорости движения тела от времени задана функцией у = f(t).
Если на интервале (2; 5) функция f(t) возрастает, то это означает, что в этот момент времени скорость тела увеличивается - на тело действует ускорение.
А интервал убывания (7; 10) говорит о том, что скорость со временем уменьшается - происходит торможение тела.
Так промежутки монотонности позволяют качественно оценить характер протекания физических процессов.
Связь возрастания и убывания с экстремумами
Если функция сначала возрастает, затем убывает, а потом снова возрастает - скорее всего, в точке перехода от роста к спаду имеется точка максимума.
А в точке смены убывания на возрастание находится точка минимума функции.
Это следует из того, что в окрестности точки максимума значения функции выше, чем справа и слева от нее. Поэтому сначала функция растет, а затем убывает после прохождения "пика".
Аналогично для точки минимума - формируется "впадина" на графике функции.
Таким образом, исследуя характер монотонности, можно локализовать кандидатов в точки экстремума функции.
Влияние выбора интервала
При исследовании монотонности функции очень важен правильный выбор интервала анализа. Одна и та же функция может вести себя по-разному на разных промежутках.
Например, рассмотрим функцию f(x) = x^3 - 3x. На интервале (-2; 5) она возрастает, а вот на промежутке (-5; 2) убывает. Поэтому, говоря о характере монотонности, всегда нужно указывать конкретный анализируемый интервал.
Свойства монотонности при арифметических операциях над функциями
Интересный вопрос - что происходит с монотонностью функций при выполнении над ними арифметических действий: сложения, вычитания, умножения и деления.
Оказывается, есть несколько полезных свойств:
- Если
f(x)иg(x)возрастают на интервале, то их сумма и произведение там тоже возрастают - Если одна функция возрастает, а другая убывает, то ничего определенного про их сумму и произведение сказать нельзя
- Частное двух положительных возрастающих (убывающих) функций также является возрастающей (убывающей) функцией
Эти свойства могут упростить исследование сложных функций, представимых как комбинации более простых.
Композиция функций и ее монотонность
Еще одна интересная операция, которая часто встречается на практике - это композиция функций. То есть построение новой функции вида f(g(x)).
Здесь также есть несколько полезных свойств:
- Если
f(x)иg(x)обе возрастают (убывают), то их композиция тоже будет возрастающей (убывающей) функцией - Но если одна функция возрастает, а другая убывает - ничего определенного о монотонности их композиции сказать нельзя
Эти свойства также упрощают работу с композициями функций.
Связь с пределами и непрерывностью
Промежутки монотонности тесно связаны с другим фундаментальным понятием математического анализа - пределом функции. Например, если функция возрастает (убывает) на промежутке, то у нее существуют конечные односторонние пределы при стремлении аргумента к концам этого интервала.
Более того, из существования этих односторонних пределов часто можно сделать вывод о характере монотонности функции вблизи заданной точки. Аналогично, непрерывность функции на интервале связана с возможностью монотонного поведения на этом промежутке. Эти важные взаимосвязи также нужно учитывать при анализе.
Похожие статьи
- Где живет слепая ясновидящая баба Нина: адрес и отзывы
- Расположение органов у человека (фото). Внутренние органы человека: схема расположения
- Особенности российской модернизации начала 20 века. История России
- Тригонометрия с нуля: основные понятия, история
- Мифы Древней Греции: краткое содержание и суть
- Примеры текстов разговорного стиля речи. Понятие и признаки разговорной речи
- Речь: классификация речи, виды и стили речи. Устная и письменная речь
