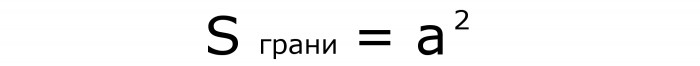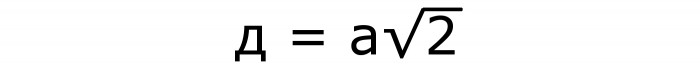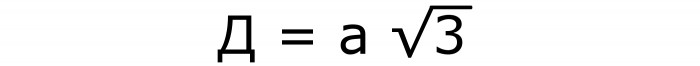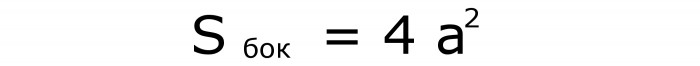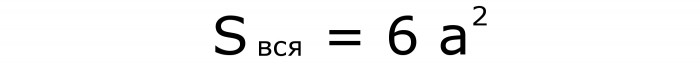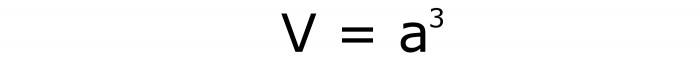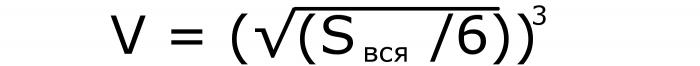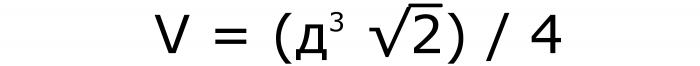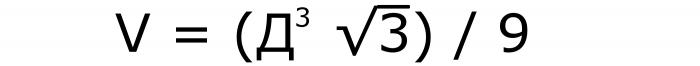Как найти объем куба: варианты задач и их решение
Современные технологии создают удивительные компьютерные программы. Они позволяют увидеть тела в объеме и покрутить их в разных направлениях, чтобы получше рассмотреть. Воображение человека не всегда на это способно. Немногие могут отчетливо представить предмет и увидеть его как бы насквозь. Но такое умение можно попытаться сформировать при решении задач по геометрии. Например, тех из них, в которых говорится о том, как найти объем куба. Это отличная практика для развития пространственного воображения.
Куб или параллелепипед?
Это непустой вопрос. Потому что классификация важна. Ведь куб — это особая форма прямоугольного параллелепипеда.
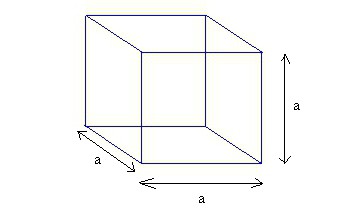
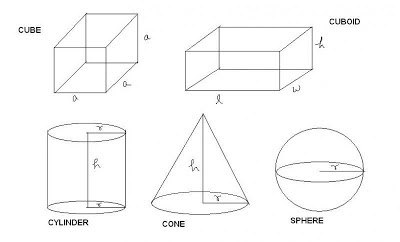
Последний представляет собой фигуру, в которой 6 граней, и все они прямоугольники. Углы, под которыми пересекаются все ребра, 90º. Соответственно, если эти грани станут квадратами, то и вся фигура преобразится в куб.
У прямоугольного параллелепипеда все линейные размеры, то есть высота, длина и ширина, могут существенно отличаться. В кубе же они всегда равны друг другу. Это его отличительный признак. Поэтому в задачах, которые требуют найти объем куба, рассмотренный момент непременно учитывается. Кстати, он существенно упрощает все математические записи и вычисления.
Условные обозначения в формулах и задачах
Без этого пункта будет сложно понять, как записаны формулы. Что подразумевается под каждой буквой и символом, подскажет следующая таблица.
| Символ | Название элемента |
| а | ребро фигуры |
| д | диагональ грани |
| Д | диагональ куба |
| общепринятые в геометрии символы | площадь |
| объем |
Как найти элементы куба по его стороне?
Поскольку грань фигуры — это квадрат, то ее площадь определится по формуле №1, в которой известную величину нужно возвести в квадрат:
А диагональ любой грани вычисляется по формуле №2, в которой сторона умножается на корень из 2:
Предыдущая формула получается из теоремы Пифагора. Это легко понять, если увидеть, что диагональ грани — это гипотенуза прямоугольного треугольника. А катетами его становятся стороны квадрата.
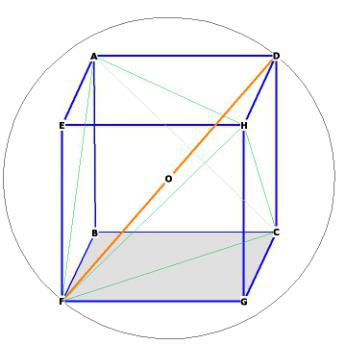
Чтобы определить диагональ куба, нужна будет следующая формула №3, содержащая известную сторону и квадратный корень из 3:
Она тоже получается из теоремы Пифагора. Только в качестве гипотенузы выступает искомая диагональ. Катетами же становятся сторона квадрата и его диагональ.
Иногда требуется знать формулу для вычисления площади боковой поверхности этой фигуры. В ней квадрат стороны умножается на 4. Вот она (№4):
Понять, как получается эта формула, несложно. Боковых граней — 4. А это значит, что их общая площадь - учетверенное значение площади одного квадрата.
Если нужно определить площадь всей поверхности, то используют эту запись, в которой ушестеряется квадрат ребра (формула №5):
Она получается аналогично предыдущей формуле, только число квадратов увеличилось до 6.
Что такое объем?
Если говорить просто, то это место, которое занимает любое тело в пространстве. Любой предмет ограничен в пространстве поверхностями. Их может быть несколько, но возможны случаи, когда только одна. Например, если тело — это шар. Но эти поверхности обязательно замкнуты. Пространство, которое занимает геометрическое тело, и будет его вместимостью, или объемом.
Единицы измерения объема
Когда речь идет о твердых телах, то единицами объема всегда будут кубические величины. К примеру, метр, сантиметр или километр в кубе. Для жидкостей приняты литры, которые выражаются через кубические дециметры. Но если они занимают очень большие объемы, то их измеряют также в кубических метрах. Например, при учете расхода воды в квартире ее считают в м3. Так получается удобнее и проще в числовом выражении.
Способ 1: узнать объем куба, если известна сторона
Это самый простой из методов, который подскажет, как найти объем куба. Он заключается в том, чтобы просто возвести значение стороны в третью степень. Другими словами, нужно умножить сторону на себя три раза. По аналогии с произвольным прямоугольным параллелепипедом, когда нужно было умножать все его линейные размеры. Формула будет записана так (№6):
Способ 2: известна площадь всей поверхности
В этом случае нужно будет разделить известную величину на 6. Из промежуточного ответа извлечь квадратный корень и возвести число в куб. Если записать это формулой, то получится следующее (№7):
Способ 3: дана диагональ грани куба
Для того чтобы узнать, как вычислить объем куба, в этом случае нужно выполнить следующие действия. Сначала возвести известное значение в куб, а потом умножить его на квадратный корень из 2 и разделить на 4. Формула для этой задачи (№8):
Это уравнение получается таким образом: известную диагональ нужно разделить на корень из двух. Потом число возвести в третью степень. После выполнения преобразований получается в числителе куб диагонали, а в знаменателе 2√2. Математика требует, чтобы под чертой не было иррационального числа. Поэтому от него избавляются путем умножения на √2. Тогда в числителе появляется √2, а в знаменателе получается 4.
Способ 4: по диагонали куба
Формула, которая подскажет, как найти объем куба, будет содержать действия: возведение в квадрат диагонали, умножение ее на корень из 3 и деление всего на 9. Она будет записана так (№9):
Аналогично предыдущей формуле, в этой записи сначала диагональ делится на корень из трех и возводится в куб. После преобразований в знаменателе также появляется иррациональность, от которой нужно уходить. Так, в числителе возникает величина √3, а под чертой — 9.
Примеры заданий
Задача первая. Дан куб с ребром 12 см. Вычислить его объем и выразить ответ в квадратных метрах.
В этом задании будет сложнее перевести ответ в другие единицы, чем решить, как найти объем куба. Для выполнения первой части задания потребуется формула, записанная под номером 6. После возведения в куб числа 12 получится ответ 1728 см3. Теперь нужно вспомнить, как перевести их в кубические метры. Для этой цели ответ нужно разделить на 100 три раза. Сотня появилась из того факта, что в одном метре именно сто сантиметров. А деление выполняется трижды, потому что единицы в задании кубические. Итак, 1728 разделенное на 100 даст 17,28. После второго деления получится 0,1728. Третье действие даст ответ 0,001728 м3. Это и есть ответ задачи: объем куба равен 0,001728 м3 .
Задача вторая. Имеется куб с площадью всей его поверхности, равной 600 дм2. Найти объем фигуры и выразить его в кубических метрах.
Для ответа на вопрос этого задания будет нужна формула номер 7. Первым действием известное число делится на 6. В ответе получается 100. Из него легко извлечь квадратный корень, он будет равен 10. Теперь десятку нужно возвести в куб. Так получается, что искомая величина равна 1000 дм3. Осталось перевести его в м3. Как и в предыдущей задаче, деление будет выполняться три раза, только делителем будет 10. Потому что в одном метре десять дециметров. После деления получается ответ равный 1 м3. Ответ: объем равен 1 м3.
Задача третья. Дан куб с длиной диагонали его грани, равной √2 мм. Нужно вычислить объем.
Восьмая формула поможет в том, как найти ответ в этой задаче. Первым делом нужно возвести в куб известную величину. Квадратный корень из 2 в третьей степени даст значение 2√2. После умножения на √2 получится число 4. Последним действием нужно его разделить на 4. Ответ: объем куба 1 мм3.
Задача четвертая. Известно, что диагональ куба равна 3 м. Требуется вычислить его объем.
Будет просто найти ответ на эту задачу по формуле под номером 9. Величину, которая дана в условии, нужно возвести в куб. Получится 27. После его деления на 9 ответ станет равен 3. И последним действием его нужно умножить на квадратный корень из 3. Ответом задачи будет 3√3 м3.
Похожие статьи
- Как узнать размер одежды? Таблица размеров одежды
- Как посчитать кубические метры пиломатериалов
- Ром "Бакарди" белый: отзывы, цены
- Как найти длину окружности: через диаметр и радиус. Терминология, основные формулы и характеристика фигуры
- «Монополия»: правила игры
- Простые и не очень способы того, как вычислить кубический корень
- Как найти корень уравнения: линейного, квадратного, кубического?