Тождество: что это такое, виды и примеры

Тождество - это математическое утверждение о равенстве двух математических выражений. Оно является одним из фундаментальных понятий алгебры и математического анализа.

Определение тождества

Формально тождество определяется как выражение вида:

A = B

где A и B - некоторые математические выражения. Это означает, что A и B представляют одно и то же выражение, хотя могут быть записаны по-разному. Иными словами, тождество утверждает эквивалентность или взаимозаменяемость выражений A и B.

Примеры тождеств

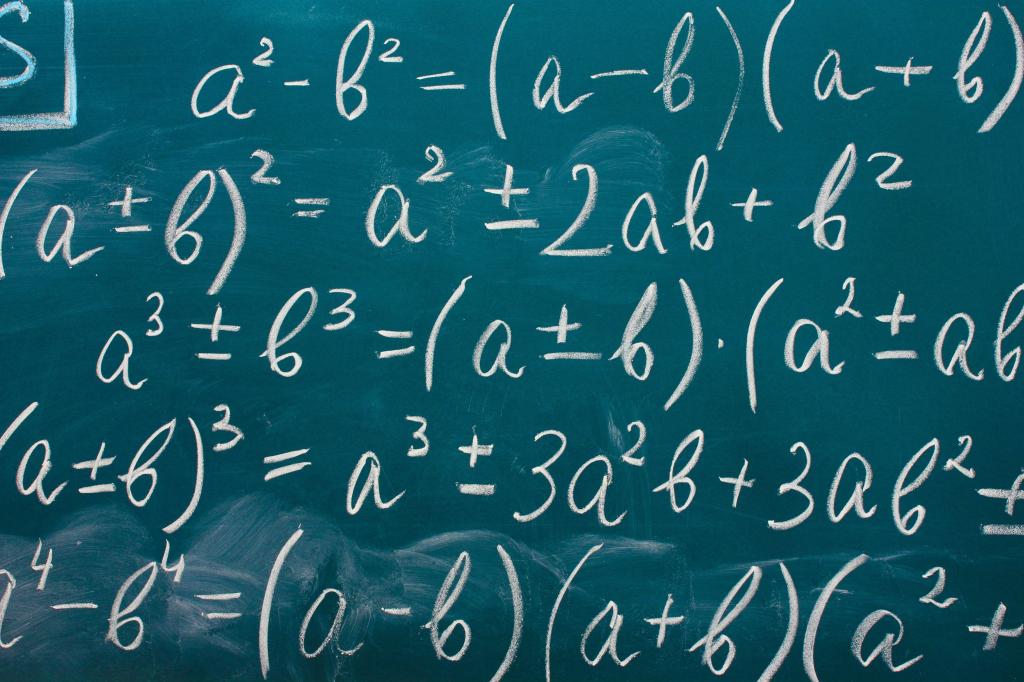
Рассмотрим несколько примеров тождеств:

• x + 0 = x
• (a + b)^2 = a^2 + 2ab + b^2 (формула разложения в сумму квадратов)
• sin^2 x + cos^2 x = 1 (тригонометрическое тождество)

Эти тождества выражают фундаментальные свойства чисел, алгебраических выражений и тригонометрических функций. Их справедливость можно проверить, подставив конкретные численные значения вместо переменных.

Доказательство тождеств

Хотя некоторые тождества очевидны или легко проверяются (как показано выше), многие тождества требуют строгого математического доказательства. Оно заключается в последовательных преобразованиях выражений A и B с использованием основных свойств чисел, функций и операций таким образом, чтобы в итоге получить равенство очевидного вида.

Например, формула для разложения в сумму квадратов выше может быть доказана следующим образом:

(a + b)^2 = (a + b)(a + b) = a(a + b) + b(a + b) = a*a + a*b + b*a + b*b = a^2 + 2ab + b^2

Здесь мы последовательно применили свойства умножения, раскрыли скобки, сгруппировали члены и так далее. В итоге пришли к исходной формуле.

Виды тождеств

Существует множество разновидностей тождеств в зависимости от того, между какими математическими объектами устанавливается равенство:

• Числовые тождества - между числами.
• Алгебраические тождества - между алгебраическими выражениями.
• Тригонометрические тождества - между тригонометрическими функциями (sin, cos и др.).
• Логарифмические тождества - с участием логарифмов.

Кроме того, различают простые тождества, которые легко проверить непосредственной подстановкой значений, и сложные - требующие доказательства с использованием различных математических правил и теорем.

Интересные факты о тождествах

• Многие великие математики внесли вклад в открытие новых тождеств, которые позволили значительно продвинуть соответствующие области математической науки.
• Тождество Эйлера для комплексных чисел связывает 5 важнейших математических констант.
• Некоторые сложные тождества требовали десятилетий кропотливых вычислений, прежде чем были наконец доказаны с применением компьютеров.

Таким образом, несмотря на кажущуюся очевидность и простоту, тождества представляют собой глубокую и фундаментальную основу всего математического знания.

Различные подходы к записи тождеств

Существует несколько способов записи тождеств в математике:

• С использованием знака равенства "=". Это самый распространенный подход, когда пишут A = B.
• При помощи символов логической эквивалентности "≡" или "~". Тогда тождество имеет вид A ≡ B.
• Словесной формулировкой: "выражение A тождественно выражению B".

Выбор того или иного способа обычно определяется контекстом и традициями конкретной области математики. Но во всех случаях речь идет об утверждении эквивалентности A и B.

Область применения тождеств

Помимо "классических" областей вроде алгебры, математического анализа и геометрии, тождества находят все большее применение в современной математике, информатике и естественных науках, в частности:

• В математической логике для записи тождественных преобразований логических формул.
• В теории алгоритмов при доказательстве эквивалентности различных способов решения одной задачи.
• В криптографии для обоснования стойкости шифров.
• В физике элементарных частиц для установления эквивалентности различных теоретических моделей.

По мере развития науки число областей, где применяются математические тождества, будет только расти.

Обобщение понятия тождества

В современной алгебре понятие тождества обобщается на произвольные алгебраические структуры помимо обычных числовых систем.

Например, если вместо чисел рассматривать матрицы или графы, то тождество между матрицами A и B означает, что у них совпадают соответствующие элементы, а тождество между графами G и H - что у них одинаковая структура ребер и вершин.

Такое обобщенное понимание позволяет перенести мощный аппарат теории тождеств на широкий класс алгебраических объектов.

Тождества в искусственном интеллекте

В задачах искусственного интеллекта, таких как распознавание образов и обработка естественного языка, тождества между объектами устанавливаются на основе вычисления меры их сходства с использованием статистических моделей.

Это позволяет приблизительно, с некоторой долей неопределенности оценить тождественность, например, двух изображений или предложений на естественном языке, что необходимо для решения практических задач.

Заключение

Тождества являются важным инструментом во многих областях математики и естественных наук. Они позволяют устанавливать глубокие связи между различными математическими объектами, упрощать сложные выражения и решать задачи. Знание основных тождеств и умение ими пользоваться - обязательная часть математической подготовки.