Ось ординат, что это за ось координат?

Прямоугольная система координат широко используется в науке и технике. Однако не все знают точное значение терминов "абсцисса" и "ордината". Давайте разберемся, что означают эти понятия и почему они так важны.
Общие сведения о системе координат
Прямоугольная система координат, в которой оси расположены под прямым углом, была введена французским математиком и философом Рене Декартом в XVII веке. Это стало настоящим прорывом в развитии геометрии и математического анализа.
Декарт в своем фундаментальном труде «Начала геометрии» описал метод координат, позволяющий переводить геометрические объекты на язык алгебры, и наоборот.
Основными элементами прямоугольной системы координат являются:
- Ось абсцисс (она же ось X) — горизонтальная ось
- Ось ординат (она же ось Y) — вертикальная ось
- Начало координат — точка пересечения осей
- Координатные четверти — 4 части плоскости
Любой точке на плоскости соответствует упорядоченная пара чисел — ее координаты (x; y). А любой паре чисел (x; y) соответствует определенная точка на плоскости с этими координатами.
| Местоположение | Координаты |
| Дом | Широта, долгота |
| Зал концертный | Номер ряда, номер места |
| Шахматная доска | Буква столбца, номер ряда |
Таким образом, система координат устанавливает взаимно-однозначное соответствие между геометрическими объектами и числами.
Абсцисса и ордината - что это такое
Итак, рассмотрим более подробно два фундаментальных понятия:
- Абсцисса
- Ордината
Это специальные термины для обозначения координат точки на плоскости. Но откуда они взялись и что означают?

Происхождение терминов
Слово «абсцисса» пришло в русский язык из французского. В свою очередь во французском оно имеет латинские корни и буквально переводится как «отрезанная линия».
Термин «ордината» также имеет латинское происхождение. На латыни ordinatus переводится как «упорядоченный, расположенный в определенном порядке».
Как не перепутать оси
Часто возникает путаница, какая из осей называется абсциссой, а какая ординатой. Вот простая ассоциация, которая поможет это запомнить:
Абсцисса начинается на букву «а» по алфавиту, ордината — на букву «о». То же самое и в латинице: сначала идет X (абсцисса), потом Y (ордината).
Еще один способ: абсцисса отвечает за горизонтальное перемещение (влево-вправо), а ордината — за вертикальное (вверх-вниз).
Значение осей координат
Итак, подведем итог:
- Ось абсцисс (ось X) - горизонтальная ось, откладывается вдоль.
- Ось ординат (ось Y) - вертикальная ось, откладывается вверх.
- Координаты оси ординат показывают высоту подъема или опускания точки относительно горизонтальной плоскости.
Зная это, легко определить координаты любой точки на плоскости. Например, для точки A(3; 5) абсцисса равна 3 (то есть отстоит от начала координат вправо на 3 единицы), а ордината равна 5 (поднялась вверх от горизонтальной плоскости на 5 единиц).
Применение координат в аналитической геометрии
Одно из важнейших применений системы координат – это аналитическая геометрия. Здесь метод координат позволяет переводить геометрические объекты (точки, прямые, кривые) на язык уравнений.
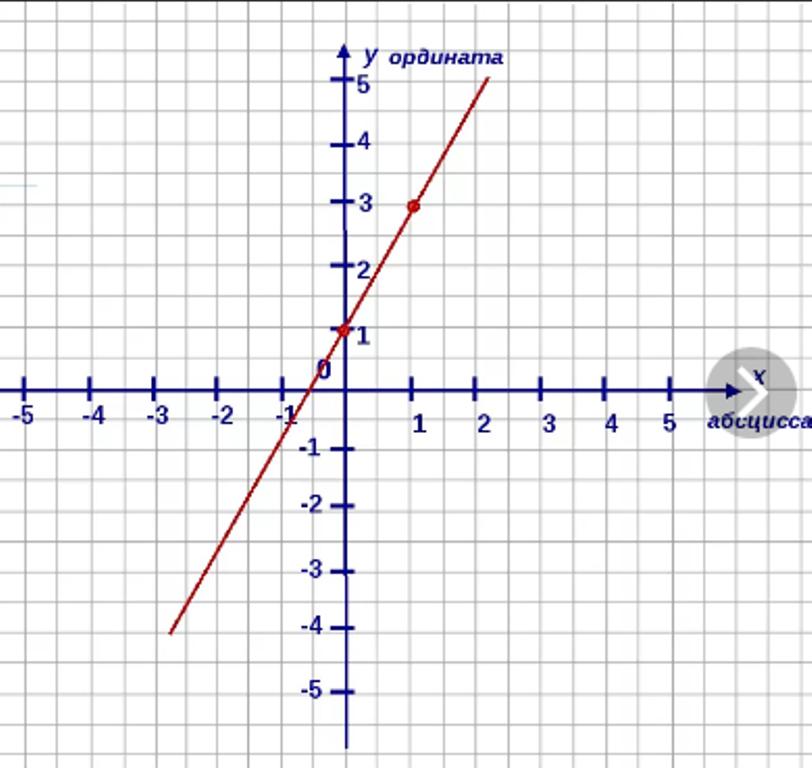
Например, уравнение прямой имеет вид:
y = kx + b
Где k и b – некоторые числа. Подставляя в это уравнение значения x и y, можно находить точки, лежащие на данной прямой. Так решаются многие геометрические задачи с помощью алгебры.
Координаты в математическом анализе
Система Декарта также послужила толчком к развитию дифференциального и интегрального исчисления. Основоположники этого направления математики – Ньютон и Лейбниц – опирались на достижения Декарта в области аналитической геометрии.
В частности, координаты активно используются при изучении функций. График функции строится в системе координат. Координаты точек графика позволяют исследовать свойства функции.
Представление векторов в координатах
Вектор задается координатами своего начала и конца. Например, вектор AB задается так:
AB = (xB - xA; yB - yA)
Где (хА; yA) – координаты точки A, (хБ; yB) – координаты точки B. Это позволяет легко выполнять операции сложения и вычитания, умножения вектора на число в координатной форме.
Применение координат в программировании
В компьютерной графике координаты точек используются повсеместно. С их помощью задаются изображения, строятся графики и диаграммы, создается анимация.
В программировании данные о координатах объектов на экране хранятся в переменных. Например, в языке Python можно записать:
x = 10 y = 5Это задаст точку с координатами (10; 5). Далее с этими переменными можно выполнять различные математические операции.
Координаты в геодезии и картографии
В геодезии для задания положения точек на поверхности Земли используется понятие географических координат – широты и долготы. Широта соответствует оси Y, долгота – оси X.
При составлении карт местности также применяется прямоугольная система координат. Координатная сетка наносится на карту для определения местоположения объектов.
Похожие статьи
- Гуманитарные профессии. Профессии социально-гуманитарного профиля
- Расположение органов у человека (фото). Внутренние органы человека: схема расположения
- Знак зодиака Скорпион (мужчина): характеристика и совместимость с другими астрологическими знаками
- Подготовительная группа по физкультуре: что нельзя делать?
- Как узнать свое тотемное животное по дате рождения
- Какие бывают предложения по цели высказывания и по интонации? Виды предложений по цели высказывания
- Парные и непарные, звонкие и глухие, мягкие и твердые согласные звуки в русском языке
