Вычисляем объемы прямых призм: формулы и примеры

Прямые призмы - одни из самых распространенных геометрических тел в окружающем нас мире. Знание формул для вычисления их объемов пригодится в быту, строительстве, проектировании и многих других сферах. В этой статье мы разберем основные формулы и приведем практические примеры расчета объемов разных видов прямых призм.

Основные понятия и определения

Призма – это многогранник, у которого две грани являются равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани – параллелограммы. Равные многоугольники называются основаниями призмы, а параллелограммы – боковыми гранями.

Различают следующие виды призм:

• По форме основания: треугольные четырехугольные пятиугольные и т.д.
• По взаимному расположению граней: прямые наклонные
• По свойствам оснований и боковых граней: правильные равнобочные равносторонние

У прямой призмы боковые ребра перпендикулярны плоскости оснований. Правильная призма имеет в основаниях правильные многоугольники, а боковые грани – квадраты.

Объем прямой треугольной призмы

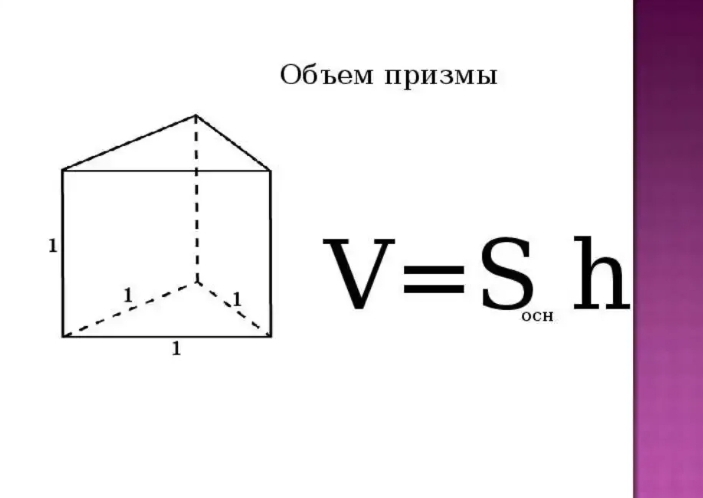
Рассмотрим более подробно формулу для вычисления объема прямой треугольной призмы и приведем несколько примеров.

У прямой треугольной призмы в основании лежит треугольник с площадью S, а боковые грани – прямоугольники. Согласно общей формуле, ее объем равен:

Рассмотрим для примера прямую призму с равносторонним треугольником в основании со стороной a и высотой H:

Площадь равностороннего треугольника вычисляется по формуле:

Подставляя это значение в формулу объема, получаем:

Для прямой треугольной призмы с прямоугольным треугольником в основании формула объема имеет вид:

где a и b – катеты прямоугольного треугольника, Н – высота призмы.

А для прямой треугольной призмы с произвольным треугольником в основании площадь этого треугольника можно найти по формуле Герона:

где а, b и с – стороны треугольника, р – полупериметр.

Вычисление объема прямой призмы с многоугольным основанием

Рассмотрим теперь, как вычислить объем прямой призмы, в основании которой лежит многоугольник - четырехугольник, пятиугольник или многоугольник с еще большим числом сторон.

Разбиение на треугольники

Любой многоугольник можно разбить на треугольники. Например, пятиугольник можно разбить на 3 треугольника (см. рисунок).

Тогда исходную многоугольную призму можно представить как сумму треугольных призм. Следовательно, ее объем равен сумме объемов составляющих ее треугольных призм:

• V_общ = V₁ + V₂ + ... + V_n

а по формуле объема прямой треугольной призмы:

• V_общ = S₁·H + S₂·H + ... + S_n·H = (S₁ + S₂ + ... + S_n)·H

Тогда окончательно получаем:

где S - площадь многоугольного основания призмы.

Прямая призма с трапецией в основании

Часто встречаются прямые призмы, у которых основание представляет собой трапецию - четырехугольник с одной парой параллельных сторон. Давайте разберем, как в этом случае вычисляется объем.

Пусть дана прямая призма с основанием - трапецией ABCD и боковым ребром H (см. рисунок). Тогда:

1. Разобьем трапецию на два треугольника с общим основанием DC.
2. Обозначим площади треугольников ADC = S1, BCD = S2.
3. Тогда общая площадь основания трапеции S = S1 + S2.
4. По формуле объема треугольной призмы, объем призмы на треугольнике ADC будет равен S1·H, а на BCD - S2·H.
5. Следовательно, общий объем призмы равен:
   V = S
   ₁
   ·H + S
   ₂
   ·H = (S
   ₁
   + S
   ₂
   )·H = S·H

То есть объем прямой призмы с трапецией в основании вычисляется по той же формуле, что и объем призмы на многоугольнике:

Вычисление объема комбинаций прямых призм

Рассмотрим теперь, как можно вычислить объем фигуры, представляющей собой комбинацию нескольких прямых призм.

Сложение и вычитание объемов

Если дана фигура, составленная из двух или более прямых призм, то ее объем равен сумме объемов составляющих призм:

• V_общ = V₁ + V₂ + ... + V_n

А если одна прямая призма частично находится внутри другой, то нужно из объема большей призмы вычесть объем меньшей:

• V_общ = V_больш - V_мал

Пример задачи

Даны две прямые призмы - куб со стороной основания 3 см и прямоугольный параллелепипед с длиной 4 см, шириной 2 см и высотой 6 см. Найти объем фигуры, изображенной на рисунке:

Решение:

1. Объем куба V_куба = a³ = 3³ = 27 см³
2. Объем прямоугольного параллелепипеда V = a·b·h = 4·2·6 = 48 см³
3. Часть куба находится внутри параллелепипеда. Найдем ее объем:
   Сторона внутреннего куба равна 2 см Тогда V
   _{внутр_куба}
   = 2
   ³
   = 8 см
   ³
4. Общий объем равен:
   V
   _общ
   = V
   _куба
   + V
   _{параллелепипеда}
   - V
   _{внутр_куба}
   = 27 + 48 - 8 =
   67 см³

Ответ: 67 см³.

Объем призмы через диагонали и углы

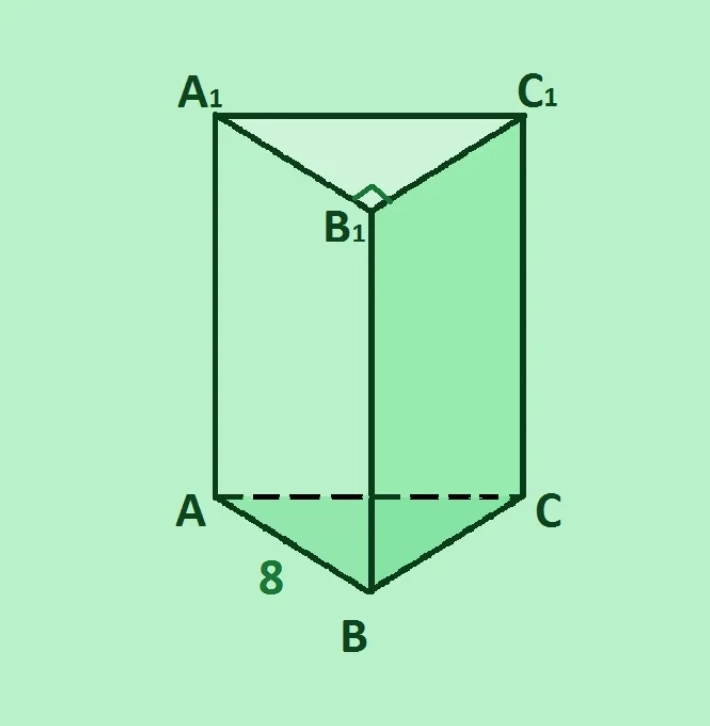
Иногда для вычисления объема прямой призмы удобно воспользоваться ее диагоналями или углами между гранями. Рассмотрим, как это сделать.

Через длину диагонали

Если известна длина диагонали прямой призмы d и угол \(\alpha\) между диагональю и плоскостью основания, то высота призмы H = d·cos\(\alpha\) (из теоремы косинусов). Объем тогда вычисляется стандартно через основание S и высоту H.

Через углы оснований

Можно также найти объем призмы, зная углы ее оснований. Например, для прямой треугольной призмы, если даны углы основания \(\alpha\), \(\beta\) и \(\gamma\), то площадь основания найдется из теоремы синусов, а объем вычислится через площадь S и высоту H как обычно.