Найти
×

Как найти площадь параллелограмма: простые формулы

0
0

Параллелограмм - одна из самых распространенных геометрических фигур. Однако далеко не все знают, как вычислить площадь параллелограмма. В этой статье мы подробно разберем несколько простых способов нахождения площади параллелограмма с помощью формул и онлайн-калькулятора.

Что такое параллелограмм?

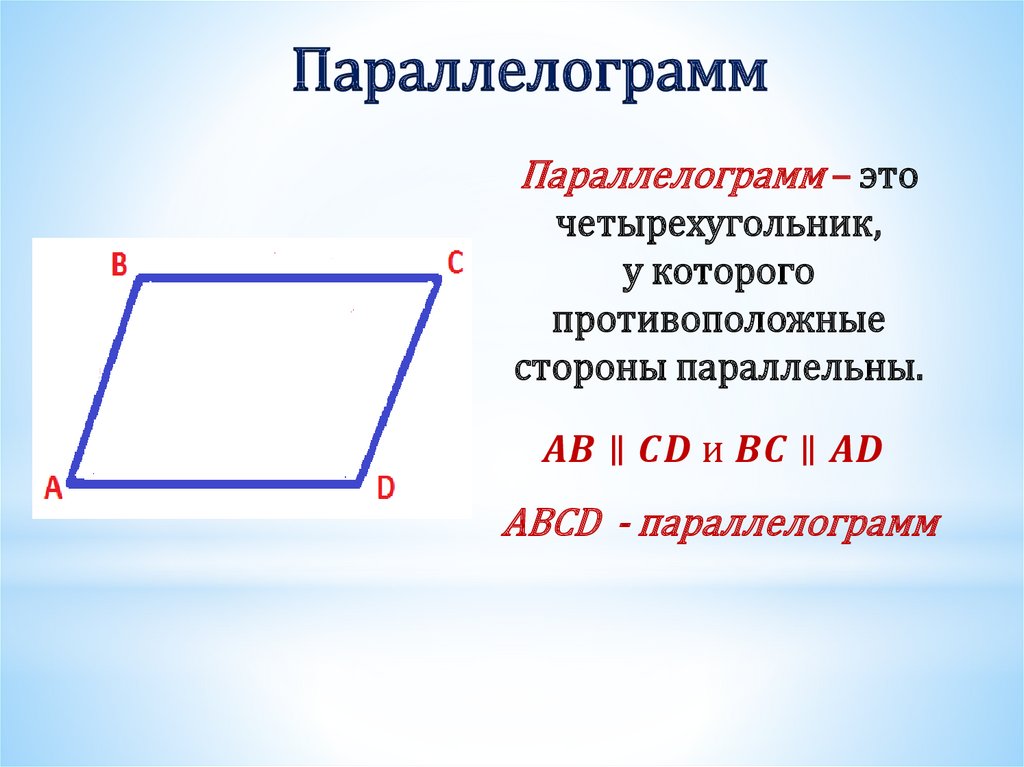
Определение параллелограмма

Давайте сначала разберемся, что из себя представляет параллелограмм. Параллелограмм - это четырехугольник, у которого противоположные стороны попарно параллельны.

То есть если соединить точки A, B, C и D, то получится четырехугольник ABCD, в котором стороны AB и CD параллельны, а стороны AD и BC тоже параллельны.

  • У параллелограмма есть несколько важных свойств: Противоположные стороны равны между собой: AB = CD, AD = BC Диагонали взаимно перпендикулярны, то есть пересекаются под прямым углом
  • Существует несколько разновидностей параллелограмма: Прямоугольник - у него все углы прямые Ромб - у него все стороны равны Квадрат - у него все углы прямые и все стороны равны

В окружающем нас мире можно найти множество примеров объектов, имеющих форму параллелограмма: рамки окон, дверные проемы, элементы конструкций зданий, поля для игры в теннис, бейсбол и другие спортивные площадки.

Формулы для вычисления площади параллелограмма

Площадь параллелограмма

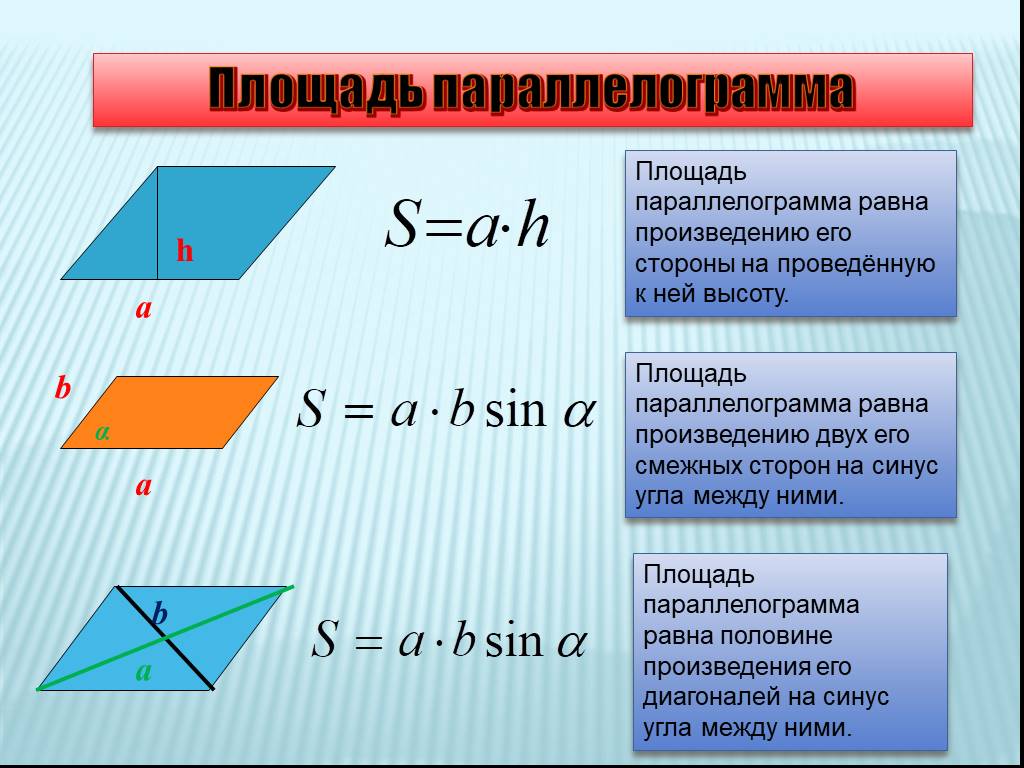
Для того, чтобы найти площадь параллелограмма, можно использовать следующие основные формулы:

  1. S = a * h, где
      S - площадь параллелограмма a - длина основания h - высота параллелограмма, проведенная к этому основанию
  2. S = a * b * sin(α), где
      S - площадь параллелограмма a и b - длины двух смежных сторон α - угол между этими сторонами
  3. S = 0.5 * d1 * d2 * sin(α), где
      S - площадь
      параллелограмма d
    1
      и d
    2
      - длины диагоналей α - угол между диагоналями

Давайте разберем подробнее каждую из этих формул для нахождения площади параллелограмма.

Первая формула вытекает из того, что любой параллелограмм можно разбить на два равных треугольника, опустив высоту h. Тогда площадь каждого треугольника равна S = (a * h) / 2 по формуле площади треугольника. А раз в параллелограмме два таких одинаковых треугольника, то его площадь S = a * h.

Вторая и третья формулы основаны на тригонометрических соотношениях в параллелограмме. Давайте разберем вывод второй формулы. Рассмотрим параллелограмм ABCD с известными сторонами a = AB и b = BC и острым углом α между ними. Из точки C опустим перпендикуляр h на сторону AB. Тогда получим прямоугольный треугольник ABC, для которого выполняется соотношение: sin(α) = h / b. Отсюда h = b * sin(α). Подставляем это выражение для высоты h в формулу первого способа: S = a * h = a * b * sin(α). Вот и получили вторую формулу!

А третья формула получается аналогично, через тригонометрические соотношения в треугольнике, образованном диагоналями параллелограмма.

Теперь давайте разберем, как выбрать нужную формулу в зависимости от исходных данных о параллелограмме, которые у нас есть в условии задачи.

Известно Формула
Основание a и высота h S = a * h
Стороны a, b и ∠α S = a * b * sin(α)
Диагонали d1, d2 и ∠α S = 0.5 * d1 * d2 * sin(α)

Примеры решения задач на нахождение площади параллелограмма

Давайте теперь на практике разберем несколько примеров, как применить рассмотренные формулы для нахождения площади параллелограмма.

Пример 1

Дан параллелограмм со стороной а = 5 см и высотой h = 3 см. Найдем его площадь S.

Решение:

В данном случае нам известны сторона а = 5 см, к которой проведена высота h = 3 см. Значит, воспользуемся первой формулой: S = a * h

Подставляя числовые значения, получаем: S = 5 см * 3 см = 15 кв.см

Ответ: S = 15 кв.см

Пример 2

Дан параллелограмм со сторонами a = 7 см, b = 8 см. Угол между этими сторонами равен α = 40°. Найти площадь параллелограмма.

Решение:

В этой задаче нам даны длины смежных сторон a и b и угол α между ними. Следовательно, используем вторую формулу:

S = a * b * sin(α)

Подставляем значения в формулу:

S = 7 см * 8 см * sin(40°)

Синус 40° равен приблизительно 0,643. Тогда:

S = 7 * 8 * 0,643 = 36 кв.см

Ответ: площадь параллелограмма равна 36 кв.см.

Пример 3

Дан параллелограмм с диагоналями d1 = 10 см, d2 = 8 см. Угол между диагоналями составляет α = 60°. Найти площадь параллелограмма.

Решение:

В задаче известны длины диагоналей d1 и d2 и угол α между ними. Следовательно, воспользуемся третьей формулой для нахождения площади параллелограмма:

S = 0.5 * d1 * d2 * sin(α)

Подставляя значения, получаем:

S = 0.5 * 10 см * 8 см * sin(60°)

Sin(60°) = 0,866. Окончательно имеем:

S = 0,5 * 10 * 8 * 0,866 = 34,64 кв.см

Ответ: S = 34,64 кв.см


Похожие статьи